Gleichwertigkeit von irgendwas
Eine Masse von 5 kg und 5000 g sind äquivalent: beide meinen dasselbe. In der Mathematik bezieht sich das Wort meist auf Terme und Gleichungen. Das wird hier kurz vorgestellt. => Ganzen Artikel lesen …
⇔ Gleichwertig
Äquivalent heißt wörtlich übersetzt: gleichwertig. Die Aussagen „x ist größer als 4“ ist äquivalent zu „x ist nie kleiner als 4 oder genau 4“ sind äquivalent. Äquivalenz kann sich auf Aussagen, Terme und Gleichungen beziehen. Lies mehr dazu unter => Äquivalenz
… in der Logik das Weder-noch, kurz das => NOR
… Energiemenge von 41,868 Megajoule => Öleinheit
… TNT-äquivalente Energiewirkung von Bomben | Siehe unter => Bomben
Mit dem TNT-Äquivalent gibt man an, wie viel Energie bei einer Explosion frei wird. Als Vergleich dient dabei die freigesetzte Energie einer bestimmten Masse des Sprengstoffes TNT, oder ausgeschrieben => Trinitrotoluol
Definition
4x-1x = 6 und 3x = 4+2 - diese zwei Gleichungen sind zueinander äquivalent. Das heißt, dass man für x jede beliebige Zahl einsetzen kann. Für eine eingesetzte Zahl sind dann beide Gleichungen entweder erfüllt (wahre Aussage) oder nicht erfüllt (falsche Aussage). Das ist hier kurz erläutert. => Ganzen Artikel lesen …
Genau dann wenn
In der Logik heißt Äquivalenz so viel wie genau-dann-wenn-Aussage. Dazu stehen hier kurz einige Beispiele => Ganzen Artikel lesen …
Definition
x+x und 2·x: Terme, bei denen immer das Gleiche herauskommt, egal welche Zahl man für x einsetzt, nennt man äquivalent zueinander. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
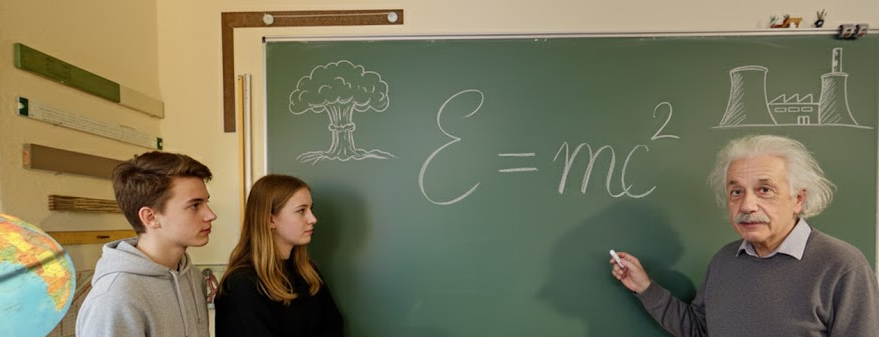 Äquivalenz von Masse und Energie
Äquivalenz von Masse und Energie
E=mc²
Diese Formel gibt an, wie viel Energie man aus einer Masse m gewinnen könnte, wenn die Masse vollständig in Energie umgewandelt wird. In der Relativitätstheorie steht der Ausdruck für die sogenanne Ruheenergie. Bei Kernumwandlungen spricht man vom Massendefizit, wenn Masse zugunsten von Materie verloren geht. => Ganzen Artikel lesen …
… in der Aussagenlogik die => Implikation
 Äquivalenzumformung
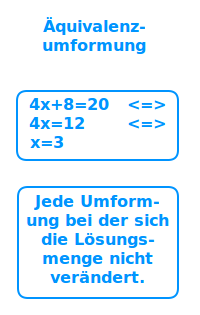
Äquivalenzumformung
⇔
Man formt eine Gleichung so um, dass sich ihre Lösungsmenge dabei nicht verändern kann. Das wird hier erklärt am Beispiel: 2·(x-4) = 12. => Ganzen Artikel lesen …
 Äquivalenzumformungen
Äquivalenzumformungen
Beispiele
Das Wort gehört zum Thema Gleichungen lösen: eine Äquivalenzumformung ist eine Umformung, bei der sich die Lösungsmenge einer Gleichung nicht ändern kann. Hier stehen einige Beispiele sowie auch Gegenbeispiele. => Ganzen Artikel lesen …
… ⇔, die Bedeutung steht unter => Äquivalenz
… in der Aussagenlogik die => Implikation
 Keine Äquivalenzumformungen
Keine Äquivalenzumformungen
Beispiele
Eine Gleichung so umzuformen, dass sich dabei die Lösungsmenge nicht verändert nennt man eine Äquivalenzumformung. Nicht alle Rechnungen sind solche Äquivalenzumformungen. Hier stehen einige wichtige Ausnahmen. => Ganzen Artikel lesen …
 Logische Äquvialenz
Logische Äquvialenz
Definition
Es ist nur genau eine Aussage wahr: entweder es stimmt die eine Aussage oder es stimmt die andere Aussage, nicht aber beide Aussagen gleichzeitig oder keine von ihnen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …

