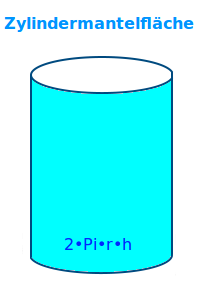
Zylindermantelfläche
M = 2·Pi·r·h
© 2016
- 2025
Basiswissen
Eine Getränkedose ist ein typischer Zylinder. Wenn man ihn gedanklich aufrecht aufstellt, dann ist unten die kreisförmige Grundfläche und oben die kreisförmige Deckfläche. Dazwischen ist der rohrförmige Mantel. Der Mantel ist dann der senkrechte Teil zwischen Grund- und Deckfläche. Als Mantelfläche oder Mantelflächeninhalt bezeichnet man nur die nach außen zeigende Fläche. Siehe auch 👉 Mantelfläche
Formeln
- M = 2·Pi·r·h
- M = Pi·d·h
Legende
- M = Mantelfläche, z. B. in cm²
- Pi = Kreiszahl, etwa 3,14
- r = Radius der Grund- oder Deckfläche (halber Durchmesser)
- d = Durchmesser der Grund- oder Deckfläche (doppelter Radius)
- h = Höhe (Strecke von Grund- zu Deckfläche)
In Worten
Multipliziere die Kreiszahl Pi (ungefähr 3,14) mit der Zahl 2. Multipliziere das Ergebnis mit dem Radius r der Grundfläche. Multiplizieren dieses Ergebnis mit der Höhe des Zylinders. Das Ergebnis ist die Zylindermantelfläche. Siehe auch 👉 Zylinderformeln