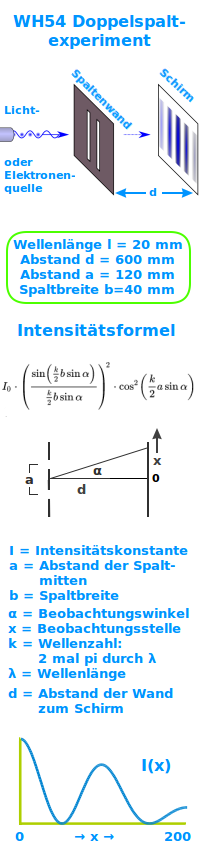
WH54 Doppelspaltexperiment

Papiermodell

Basiswissen · Die Grundfläche: DIN-A1 · Die Licht- oder Elektronenquelle · Die Wand mit den Spalten · Der Projektionsschirm · Die verwendete Formel als Pseudocode · Was meint Pseudocode? · Wie wirkt sich die Spaltbreite b aus? · Wie wirkt sich der Spaltabstand a aus? · Wie wirkt sich die Wellenlänge l aus? · Was sind gute Werte für eine Tisch-Simulation? · Wie sieht das Interferenzmuster aus? · Wie berechnet man den Abstand der Maxima? · Was sind die Funktionswerte für I(x)? · Was ist die si-Funktion?

Basiswissen

Das Doppelspaltexperiment als makroskopisches Modell (etwa 400 mm langer Schirm) zum anschaulichen Berechnen eines Interferenz-Musters. Die Wellenlänge ist 2 cm. Damit entstehen Maxima die etwa 10 cm voneinander entfernt sind.

Bildbeschreibung und Urheberrecht — Aufbau und die Intensitätsformel © Johannes Kalliauer [Wikimedia Commons] ☛

Die Grundfläche: DIN-A1

Die Grundfläche hat das Papierformat: DIN-A1

Die Länge beträgt 841 Millimeter, die Breite 594 Millimeter.

Die Grundfläche wird im Querformat gedacht.

Die linke obere Ecke ist dann der Nullpunkt eines Koordinatensystems.

Die x-Achse geht von links nach rechts, die y-Achse von oben nach unten.

Die Angaben der Werte sind in Millimetern.

Die Licht- oder Elektronenquelle

Sie steht auf den Koordinaten: (100|420,5)

Sie kann dargestellt werden durch einen kleinen Stift oder eine Kugel.

Es genügt, wenn die Lichtquelle markiert ist, sie hat sonst keine Funktion.

Die Wand mit den Spalten

Die Wand kann aus Pappe gebastelt sein.

Die Wand sollte von alleine aufrecht stehen können.

Die Höhe sollte bei etwa 50 mm liegen.

Die Wand wird parallel zur y-Achse aufgestellt.

Sie geht bei x=200 mm durch die x-Achse.

Der Projektionsschirm

Der Schirm wird analog zur Wand mit den Spalten gebaut.

Er sollte von alleine aufrecht stehen können.

Seine Höhe soll bei etwa 50 mm liegen.

Er wird bei x=800 mm platziert.

Die verwendete Formel als Pseudocode

zaehler_links=sin((k/2)*b*sin(alpha))
nenner_links=(k/2)*b*sin(alpha)
faktor_links=(zaehler_links/nenner_links)^2
klammer_rechts=(k/2)*a*sin(alpha)
faktor_rechts=(cos(klammer_rechts))^2
intensitaet=faktor_links*faktor_rechts

Was meint Pseudocode?

Code bedeutet hier: Programmierquelltext

Die vollständige Formel ist als Fließtext unübersichtlich.

Der Pseudocode formuliert sie als Basic-Programm (Programmiersprache).

Das Formel kann zum Beispiel als Teil eines Basic-Programmes verwendet werden.

Programm kann beispielsweise direkt in Basic256 ausgeführt werden.

Mehr dazu unter Basic256 Programme WH54 Doppelspaltexperiment ↗

Wie wirkt sich die Spaltbreite b aus?

Eine Änderung der Spaltbreite b führt zu einer Änderung der Lage der Extrema des Einfachspaltes, dessen Intensitätsverteilung die Hüllkurve der Intensitätsverteilung des Doppelspalts bildet → Je breiter der Spalt, desto enger wird die Hüllkurve

Wie wirkt sich der Spaltabstand a aus?

Eine Änderung des Spaltabstandes a führt zu einer Änderung der Lage der Extrema des Doppelspalts innerhalb der konstant bleibenden Hüllkurve → Je größer der Spaltabstand, desto enger liegen die Extrema des Doppelspalts beieinander

Wie wirkt sich die Wellenlänge l aus?

Eine Änderung der Wellenlänge λ wirkt sich sowohl auf die Hüllkurve als auch auf die Intensitätsverteilung des Doppelspalts aus → Je größer die Wellenlänge, desto breiter werden Hüllkurve und die Interferenzabstände des Doppelspalts

Was sind gute Werte für eine Tisch-Simulation?

Wellenlänge l = 20 mm

Abstand d = 600 mm

Abstand a = 120 mm

Spaltbreite b=40 mm

Wie sieht das Interferenzmuster aus?

Das Muster wird beschrieben von der Schirmmitte bis zu einem Abstand x von 200 mm.

Je näher an der Schirmmitte (x=0), desto größer die Maxima.

In diesem Bereich sieht man drei Maxima und zwei Minima.

Die Maxima liegen etwa 10 cm voneinander entfernt.

Wie berechnet man den Abstand der Maxima?

Die Maxima sind die am intensivsten beleuchteten Stellen auf dem Schirm.

Sie sind im Graph die Hochpunkte der sinusartigen Kurve.

Es gibt eine Formel zur Berechnung des Abstandes benachbarter Maxima:

Abstand benachbarter Maxima = l·(d/a)

Mit l = 20 mm, d = 600 mm und a = 120 mm erhält man:

Abstand in mm = 20·600:120 = 100 mm

Das passt sehr gut zu den Werten unten.

Was sind die Funktionswerte für I(x)?

Spalte 1: x-Position auf dem Schirm (Abstand von Schirmmitte)

Spalte 2: Intensität mit Intensitätsfaktor I₀ = 1

1 | 0.998977

2 | 0.995912

3 | 0.990818

4 | 0.983717

5 | 0.974639

6 | 0.963623

7 | 0.950715

8 | 0.935972

9 | 0.919454

10 | 0.901233

11 | 0.881386

12 | 0.859997

13 | 0.837155

14 | 0.812958

15 | 0.787507

16 | 0.760909

17 | 0.733275

18 | 0.704721

19 | 0.675366

20 | 0.645332

21 | 0.614742

22 | 0.583723

23 | 0.552402

24 | 0.520907

25 | 0.489366

26 | 0.457906

27 | 0.426654

28 | 0.395736

29 | 0.365272

30 | 0.335384

31 | 0.306188

32 | 0.277797

33 | 0.25032

34 | 0.22386

35 | 0.198517

36 | 0.174385

37 | 0.15155

38 | 0.130093

39 | 0.11009

40 | 0.091608

41 | 0.074707

42 | 0.059442

43 | 0.045857

44 | 0.03399

45 | 0.023873

46 | 0.015526

47 | 0.008966

48 | 0.004198

49 | 0.001221

50 | 0.000027

51 | 0.000598

52 | 0.002912

53 | 0.006935

54 | 0.012631

55 | 0.019952

56 | 0.028849

57 | 0.039261

58 | 0.051125

59 | 0.064371

60 | 0.078924

61 | 0.094704

62 | 0.111627

63 | 0.129603

64 | 0.148542

65 | 0.168347

66 | 0.188921

67 | 0.210164

68 | 0.231975

69 | 0.254249

70 | 0.276884

71 | 0.299775

72 | 0.322818

73 | 0.34591

74 | 0.368948

75 | 0.391831

76 | 0.414461

77 | 0.43674

78 | 0.458575

79 | 0.479875

80 | 0.500552

81 | 0.520522

82 | 0.539707

83 | 0.558031

84 | 0.575423

85 | 0.591817

86 | 0.607154

87 | 0.621377

88 | 0.634436

89 | 0.646288

90 | 0.656893

91 | 0.666219

92 | 0.674238

93 | 0.680929

94 | 0.686277

95 | 0.690271

96 | 0.692908

97 | 0.694189

98 | 0.694121

99 | 0.692717

100 | 0.689995

101 | 0.685978

102 | 0.680692

103 | 0.674171

104 | 0.666452

105 | 0.657576

106 | 0.647587

107 | 0.636535

108 | 0.624471

109 | 0.611452

110 | 0.597535

111 | 0.582781

112 | 0.567252

113 | 0.551015

114 | 0.534134

115 | 0.516677

116 | 0.498714

117 | 0.480314

118 | 0.461546

119 | 0.442479

120 | 0.423184

121 | 0.403728

122 | 0.384181

123 | 0.364609

124 | 0.345078

125 | 0.325652

126 | 0.306393

127 | 0.287361

128 | 0.268614

129 | 0.250208

130 | 0.232196

131 | 0.214627

132 | 0.19755

133 | 0.181008

134 | 0.165042

135 | 0.149691

136 | 0.134988

137 | 0.120965

138 | 0.107649

139 | 0.095065

140 | 0.083234

141 | 0.072172

142 | 0.061894

143 | 0.05241

144 | 0.043728

145 | 0.03585

146 | 0.028778

147 | 0.022509

148 | 0.017038

149 | 0.012355

150 | 0.00845

151 | 0.005308

152 | 0.002912

153 | 0.001244

154 | 0.000282

155 | 0.000002

156 | 0.000379

157 | 0.001386

158 | 0.002993

159 | 0.005171

160 | 0.007886

161 | 0.011107

162 | 0.0148

163 | 0.018929

164 | 0.02346

165 | 0.028356

166 | 0.033581

167 | 0.0391

168 | 0.044875

169 | 0.050871

170 | 0.057052

171 | 0.063382

172 | 0.069826

173 | 0.07635

174 | 0.082921

175 | 0.089506

176 | 0.096073

177 | 0.102592

178 | 0.109034

179 | 0.115371

180 | 0.121577

181 | 0.127625

182 | 0.133493

183 | 0.139158

184 | 0.144599

185 | 0.149798

186 | 0.154737

187 | 0.1594

188 | 0.163773

189 | 0.167843

190 | 0.1716

191 | 0.175033

192 | 0.178136

193 | 0.180903

194 | 0.183327

195 | 0.185408

196 | 0.187142

197 | 0.188531

198 | 0.189574

199 | 0.190275

200 | 0.190637

Was ist die si-Funktion?

Die si-Funktion, auch sinc(x) geschrieben hat als Funktionsterm f(x)=sin(x)/x, kann durch Graphentransformationen auf reale Interenzmuster auf dem Schirm angepasst werden. Sie ist damit eine beschreibende Interferenzmuster-Funktion. x ist dabei eine Positin auf dem Schirm oder der Wandund f(x) ist dann die Lichtinenstität, die man bei diesem x-Wert beobachtet. Zur Mathematik siehe unter Si-Funktion ↗