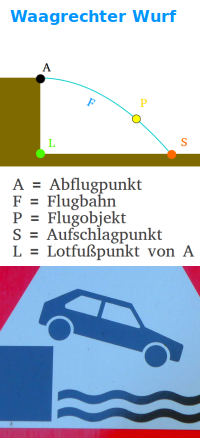
Waagrechter Wurf
Definition
Basiswissen
Wird ein Gegenstand parallel zur Erdoberfläche abgeworfen, spricht man von einem waagrechten oder auch horizontalen Wurf. Das ist hier mit Formeln ausführlich erklärt.
Annahmen zum waagrechten Wurf
Der waagrechte Wurf bezeichnet üblicherweise einen Wurf unter Vernachlässigung des Luftwiderstandes. Auch wird die Fallbeschleunigung der Erde als konstant angenommen (g=9,81 m/s²). Auf den geworfenen Körper - das Projektil - wirken alleine seine Trägheit und die Schwerkraft. Die Schwerkraft wird dabei als immer gleich stark und als in die gleiche Richtung zeigend angenommen, meist zum Erdmittelpunkt hin. Der waagrechte Wurf ist damit ein besonderer freier Fall ↗
Formeln zum waagrechten Wurf
- x-Beschleunigung zur Zeit t: ax = 0
- y-Beschleunigung zur Zeit t: ay = g
- x-Geschwindigkeit zur Zeit t: vx = konstant
- y-Geschwindigkeit zur Zeit t: vy = g·t
- x-Position zur Zeit t: sx = vo · t
- y-Position zur Zeit t: - sy = 0,5·g·t²
- Wurfweite: smax = vo · Wurzel (2·ho/g)
- Fallhöhe: ymax = g·(xmax)²/(2·vo²)
- Wurfdauer: tmax = Wurzel (2·hmax/g)
- Aufprallwinkel: tan(b) = vy/vx
- Mehr unter waagrechten Wurf berechnen ↗
Fall mit Luftwiderstand
Betrachtet man auch den Luftwiderstand, dann wird aus dem freien Fall ein zunächst beschleunigter, dann gebremster und am Ende ein Fall mit einer konstanten Fallgeschwindikeit. Oft betrachtet man zunächst auch nur den senkrechten Fall geradewegs nach unten. Das klassische Beispiel ist der Sprung eines Fallschirmspringers aus einem Flugzeug. Die konstante Endgeschwindigkeit liegt dann in der Gegend von 200 Kilometern pro Stunde. Siehe auch Fall mit Luftwiderstand ↗
Fall ohne Luftwiderstand mit verändlichem g
Wird beim Fall auch die sich verändernde Erdbeschleunigung berücksichtigt, betrachtet man die sogenannte Keplerbahn. Die sich ergebenden Bewegungslinien bezeichnet man als Trajektorien. Einen solchen Fall hat man zum Beispiel bei der Annäherung einer antriebslosen Raumsonde an einen Mond oder Asteroiden ohne Gashülle. Siehe mehr dazu unter Keplerbahn ↗
Fall mit Luftwiderstand und veränderlichem g
Betrachtet man einen Fall aus sehr großer Höhe, etwa den Absturz eines Satelliten, den Wiedereintritt einer Raumfähre in die Erdatmosphäre oder den Sturz eines Meteoriten auf die Erde, so muss man zusätzlich zur Wirkung der Lufthülle auch noch berücksichtigen, dass hier die Anziehungskraft der Erde mit sinkender Höhe immer stärker wirkt. Solche durchaus sehr komplizierten Fälle betrachtet man in der Ballistik ↗
Fußnoten
- [1] Schon Galileo hat recht exakte Versuche über den waagrechten Wurf angestellt. Bei vierfacher Absprunghöhe würde sich die Flugweite verdoppeln. Das passt gut auf die modernen Gesetze. In: Jürgen Teichmann: Wandel des Weltbildes. Astronomie, Physik und Meßtechnik in der Kulturgeschichte. Mit Beiträgen von Volker Bialas und Felix Schmeidler. Wissenschaftliche Buchgesellschaft. Darmstadt. Dort die Seiten 143 und 144.
- [2] Von Galilei sind Skizzen überliefert, aber keine Messreihen, in denen man verschiedene Flugbahnen von einem gemeinsamen Absprungpunkt am Ende einer waagrechten Absprungschanze sieht. In: St. Drake: Galileo's experimental confirmation of horizontal inertia: Unpublished manuscripts. In: Isis, Band 64, 1973, Seiten 291 bis 305.
- [3] Wie aus einem waagrechten Wurf durch immer höhere Abschussgeschwindigkeiten am Ende ein Satellit wird, nämlich eine immerwährende Kreisbahn um die Erde, zeigte ein Bild von Isaac Newton aus dem Jahr 1687. Vom Gipfel eines hohen Berges auf einer Erdkugel gehen horizontal (waagrecht) mehrere parabelartig nach unten weisende Linien weg. Immer weiter gestreckte Parabeln werden letzendlich zu einem Kreis. In: Philosophiae naturalis principia mathematica. London. 1687.
