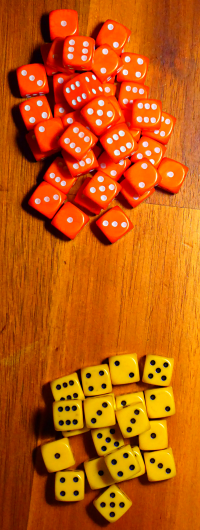Basiswissen

Schritt 1

• Aufbau:
  

• Man hat zwei Haufen Spielwürfel aus Kiste 8 ↗
  

• Auf dem Haufen A liegen 40 Würfel.
  

• Auf dem Haufen B liegen 20 Würfel.
  

Schritt 2

• Übergänge:
  

• Vom Haufen A werden alle geworfenen 6er weggenommen.
  

• Vom Haufen B werden alle geraden Zahlen weggenommen.
  

• Dann die 6er von A zum Haufen B hinzufügen.
  

• Und die geraden Zahlen von B zu A hinzufügen.
  

• Dieses Vorgehen dann ständig wiederholen.
  

Schritt 3

• Rückblick:
  

• Irgendwann behalten die Haufen trotz der Übergänge in etwa ihre Anzahl Würfel.
  

• Ab dem wievielten Schritt stellt sich das ein?
  

• Wie könnte man das vorausberechnen?
  

Tipp

• Es stellt sich schon nach wenigen Schritten eine ziemlich stabile Verteilung ein.
  

• In einem Testlauf schwankten die realen Zahlen um 1 bis 2 um den berechneten Wert.
  

Zur Theorie