Versuch Pendeldauer Amplitude
Anleitung
© 2016
- 2025
Basiswissen
Benötigt ein Pendel mehr Zeit, wenn es weniger weit schwingen muss? Dieser Frage wird hier mit einem einfachen Versuch untersucht. Die Antwort hat viele Experimentatoren sehr verblüfft. Das Ergebnis ist eher unerwartet. Am Ende steht eine Hinweis zur Auswertung. Hier folgt zunächst eine Schritt-für-Schritt Anleitung.
Grundidee
Um einmal ganz hin und her zu schwingen braucht ein Pendel immer dieselbe Zeit, egal wie stark man es anstößt und wie weit es dann schwingt. Solange man die Länge des Pendels nicht verändert, bleibt die Zeitdauer für eine Schwingung immer dieselbe. Das wird hier mit Messungen betrachtet. Der Versuch eignet sich für Kinder ab dem Vorschulalter, wenn man keine komplizierten Messungen macht. Mit Messungen sollten die Kinder etwa 12 Jahre oder älter sein.
Vorbereitung
Für diesen sehr einfach durchzuführenden Versuch benötigt man: einen Faden, ein Gewicht und eine Stoppuhr. Das Ergebnis ist eine Tabelle mit Pendelaudern für verschiedene Amplituden (Pendelausschläge). Die Anleitung unten bezieht sich auf die Einrichtung der Mathe-AC Lernwerkstatt Mathematik in Aachen. Der Versuch kann aber ohne Einschränkung mit einem selbstgefertigen Fadenpendel durchgeführt werden.
Schritt 1
- Irgendwo im Raum sollte ein Pendel von oben herabhängen.
- Es sollte etw 2 bis 3 Meter lang sein.
- Das Pendel besteht aus einem langen dünnen Faden und einem Metallgewicht.
- Das Metallgewicht ist ganz unten angebracht und schwer.
- Wenn das Pendel bewegungslos herabhängt ist es in der Ruhelage.
- Nimm jetzt das Metallgewicht in die Hand.
- Ziehe es etwa einen Zeigefinger weit aus der Ruhelage heraus.
- Das sind ungefähr 10 Zentimeter.
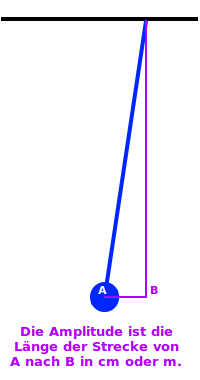
- Diese Strecke von etwa 10 Zentimeter nennt man auch die Amplitude A.
- Die Amplitude sagt, wie weit das Pendel aus der Ruhelage entfernt wurde.
- Lasse jetzt das Pendel gehen. Es schwingt nun hin und her.
- Einmal ganz hin und her nennt man eine Schwingung.
- Wie lange das Pendel für eine Schwingung braucht nennt man Schwingungsdauer T.
- Die Frage ist nun, ob sich die Schwingungdauer verändert,
- wenn man die Amplitude größer oder kleiner macht.
Schritt 2
- Versuchsblatt:
- Nimm ein leeres DIN-A4-Blatt.
- Lege es im Hochformat vor dich.
- Lasse links einen Rand von einer halben Zeigefingerlänge.
- Schreibe oben groß die Überschrift darauf: "Versuch Pendeldauer Amplitude".
- Schreibe etwas darunter deinen Namen und das Datum.
- Fertige noch weiter darunter eine Skizze des Pendels in Ruhelage an.
- Die Ruhelage meint, dass das Pendel ruhig senkrecht herunterhängt.
- Beschrifte auch: "Decke", "Faden", "Metallgewicht".
- Schreibe "Ruhelage" an das Pendel.
- Miss jetzt mit einem Meterstab die Länge des Pendels.
- Die Länge meint: von der Decke bis zur unteren Spitze des Metallgewichtes.
- Schreibe in die Nähe des Fadens "Länge l = " und dahinter die Länge in cm.
- Gehe nun etwas unter die Skizze. Schreibe dort auf:
- Amplitude etwa 10 Zentimeter, Dauer für 10 Schwingungen: _______
- Amplitude etwa 20 Zentimeter, Dauer für 10 Schwingungen: _______
- Amplitude etwa 30 Zentimeter, Dauer für 10 Schwingungen: _______
- Amplitude etwa 40 Zentimeter, Dauer für 10 Schwingungen: _______
- Amplitude etwa 50 Zentimeter, Dauer für 10 Schwingungen: _______
Schritt 3
- Versuchsdurchführung
- Nimm nun eine Stoppuhr, ideal ist eine 👉 Laboruhr
- Bewege das Pendel etwa 10 Zentimeter von der Ruhelage weg.
- Wenn du es gehen lässt, dann startest du die Stoppuhr.
- Miss genau die Zeit für 10 ganze Schwingungen.
- Eine ganze Schwingung meint eine ganze Hin-und-Her-Bewegung.
- Trage die gemessene Zeit in das Versuchsblatt ein.
- Gehe auf gleiche Weise für die anderen Amplituden vor.
Auswertung
Mit der nun erstellten Tabelle kannst du das Pendel theoretisch betrachten: gibt es für verschiedene Amplituden auch verschiedene Pendeldauern? Falls ja, dann würde man sagen, dass die Amplitude die Pendeldauer beeinflusst. Falls die Pendeldauer aber für alle Amplituden (fast) gleich ist, dann kann man sagen: die Pendeldauer hängt nicht von der Amplitude ab. Versuche anhand deiner Messdaten selbst zu entscheiden, welcher der beiden Fälle eher zutrifft.
Graph zeichnen
Aus der Tabelle kann ein Funktionsgraph erstellt werden. Die Amplituden sind die x-Werte, die dazugehörigen Dauern der y-Wert. Der Graph sollte dann eine waagrechte Gerade geben. Die Gerade verläuft also in immer gleicher Höhe parallel zur x-Achse. Was das bedeutet, kannst du nachlesen unter 👉 waagrechte Gerade