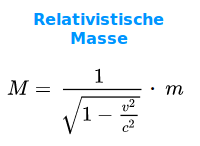Basiswissen

Als relativistische Masse M wird oft das Produkt aus dem Lorentzfaktor γ und der Ruhemasse m bezeichnet. Die relativistische Masse M ist immer größer oder gleich groß wie die Ruhemasse m. Die relativistische Masse ist der Anteil an Energie eines Teilchens, das von der Teilchengeschwindigkeit abhängt. Das Wort ist zwar weit verbreitet^[2]^[5], wird aber auch kritisiert.

Bildbeschreibung und Urheberrecht — Der Bruch links ist der Lorenztfaktor. Dieser Faktor ist immer größer oder gleich 1. Multipliziert mit der Ruhemasse m ergibt er die sogenannte relativistische Masse M. Der Begriff gilt heute als problematisch.☛

Einstein spricht sich gegen die Verwendung aus

„Es ist nicht gut, von der Masse M = m/[Wurzel aus (1 − v²/c²)] eines bewegten Körpers zu sprechen, da für M keine klare Definition gegeben werden kann. Man beschränkt sich besser auf die „Ruhe-Masse“ m. Daneben kann man ja den Ausdruck für momentum und Energie geben, wenn man das Trägheitsverhalten rasch bewegter Körper angeben will.“^[1]

Philip Gibbs spricht sich gegen die Verwendung aus

Philip E. Gibbs wurde im Jahr 1985 an der Universität Glasgow promoviert und arbeite anschließend als Softwareingenieur in verschiedenen Forschungs Einrichtungen (z. B. Desy). Gibbs betrachtet die relativistische Masse als ein Maß für die Energie eines Teilchens, die sich mit der Geschwindigkeit ändert^[3]. Diese relativistische Masse gelte nicht als Masse im eigentlichen Sinn. Der modernen Terminologie gilt als Masse ausschließlich die von der Geschwindigkeit unabhängige (Ruhe)Masse. Diese ist zum Beispiel für ein Photon immer Null. Siehe auch Lichtmasse ↗

Stephen Hawking sieht sie als gegeben an

Stephen Hawking (1942 bis 2018) geht von einer realen Zunahme der Masse mit wachsender Geschwindigkeit aus: "Je mehr sich das Objekt der Lichtgeschwindigkeit nähert, desto rascher wächst seine Masse, so daß mehr und mehr Energie erforderlich ist, es noch weiter zu beschleunigen^{[4, Seite 36]}."

Anmerkung

Einstein verwendet das Wort momentum hier im Sinne von Impuls. Die Alternativen, die er vorschlägt, sind Terme zur Berechnung eines relativistischen Impulses und einer relativistischen Energie. Dieser Handhabung folgen zunehmend viele Lehrbücher und Fachartikel.

Relativistischer Impuls ↗

Relativistische Energie ↗

Fußnoten

– [1] Albert Einstein: Brief an Lincoln Barnett: Lev B. Okun: The Concept of Mass. In: Physics Today. 43, 32 (1989). DOI: 10.1063/1.881171

[2] Richard T. Weidner, Robert L. Sells: Elementare moderne Physik. Verlag Friedrich Vieweg & Sohn. Ausgabe von 1982. ISBN: 3-528-08415-4: das Wort relativistische Masse wird verwendet und auch begründet rechtfertigt: In der Beziehung "p=mv" ist "m die sogenannte relativistische Masse. Definitionsgemäß ist die relativistische Masse m eines Teilchens diejenige physikalische Größe, mit der wir die Geschwindigkeit v multiplzieren müssen, um die Vektorgröße p zu erhzalte, dabei soll der Gesamtimpuls Σp eines abgeschlossenen Systems erhalten bleiben."

[3] Philip E. Gibbs: Does light have matter? Deutsches Elektronen-Synchrotron DESY. FAQ Seiten Physik. 1997. Online: https://www.desy.de/user/projects/Physics/Relativity/SR/light_mass.html

[4] Stephen Hawking: Eine kurze Geschichte der Zeit. Die Suche nach der Urkraft des Universums. Englischer Originaltitel: A Brief History of Time. From the Big Bang to Black Holes. Deutsch im Rohwolt Taschenbuch Verlag. 1988. ISBN: 3-499-188-50-3.

[5] Von einem "relativistischen Massenzuwachs" im Zusammenhang mit der Überlichtgeschwindigkeit sprich das: Lexikon der Physik in sechs Bänden. Walter Greulich (Herausgeber). Spektrum Akademischer Verlag, 1998-2000. ISBN: 3860252917. Dort im Artikel "Überlichtgeschwindigkeit".