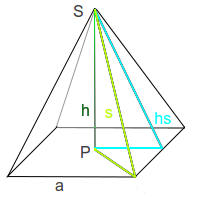
Pyramidenoberfläche
A = G + A₁ + A₂ + A₃ + A₄
© 2016
- 2026
Basiswissen
Alle Seitenflächen A sowie auch die Grundfläche G zusammengedacht ergeben die Oberfläche der Pyramide. Ihr Inhalt wird über die Addition aller Teilflächen berechnet. Einfach gesagt: alles was man von außen anstreichen könnte zählt zur Oberfläche der Pyramide.
Definition
- Die Pyramidenoberfläche setzt sich aus allen äußeren Teilflächen zusammen.
- Die Grundfläche ist per Definition immer ein Vieleck, meit ein Quadrat.
- Von der Grundfläche aus gehen die sogenannten Mantelteilflächen nach oben zur Spitze.
- Die einzelnen Teile der Mantelfäche sind immer Dreiecke.
- Grundfläche und Mantelteilflächen zusammen ergeben die Oberfläche.
- Mehr Definitionen unter 👉 Pyramide
Formeln
- A = G + A₁ + A₂ + A₃ + A₄
- A = G + M
Legende
- A = Pyramidenoberfläche
- G = Grundfläche [Boden]
- A₁ = Eine der Seitenflächen
- A₂ = Eine andere Seitenfläche
- A₃ = Eine andere Seitenlfäche
- A₄ = Eine andere Seitenfläche
- M = A₁ + A₂ + A₃ + A₄ 👉 Mantelfläche
Grundfläche
- Man berechnet erst den Flächeninhalt der Grundfläche.
- Bei einem Quadrat ist das: Bodenlänge hoch zwei.
- Ansonsten siehe unter 👉 Flächenformeln
Mantel
- Der Mantel (Vom Boden zur Spitze) setzt sich immer aus Dreiecken zusammen.
- Der Flächeninhalt eines Dreiecks ist: ½·g·h
- Mehr unter 👉 Dreiecksfläche berechnen
Einheiten
- Typische Einheiten sind cm² und m².
- Siehe auch 👉 Flächenmaße
Kuriosum
Die vier Seiten der ägyptischen Cheops-Pyramide waren früher mit weißem Kalkstein bedeckt. Die Pyramiden strahlen damit hellweiß in der Wüste. Erst später sind die weißen Platten aus Kalkstein abgerutsch oder sie wurden als Material für andere Bauten abgetragen. Siehe auch 👉 Cheops-Pyramide