Basiswissen

Definition

• Mittelwert meint hier ein arithmetisches Mittel ↗
  

• Und zwar: das arithmetische Mittel von Funktionswerten.
  

• Funktionswerte sind die f(x)- oder y-Werte einer Funktion.
  

• Mehr unter Mittelwert von Funktionswerten ↗
  

Intervall

• Man berechnet den Mittelwert immer für ein geschlossenes Interfall.
  

• Intervall meint: von einem x-Wert links bis zu einem x-Wert rechts.
  

• Den linken x-Wert nennt man meistens a, den rechten x-Wert b.
  

• Geschlossen heißt: die Randwert gehören zum Intervall dazu.
  

• Siehe auch geschlossenes Intervall ↗
  

Berechnung

• Man berechnet das bestimmte Integral von f(x) von a bis b.
  

• Man dividiert das Ergebnis durch die Differenz b-a.
  

• Das Ergebnis ist der Mittelwert der Funktionswerte.
  

• Siehe auch Bestimmtes Integral berechnen ↗
  

Anschaulich

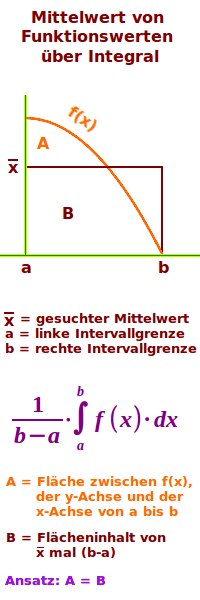
• Der gesuchte Mittelwert ist durchschnittliche Höhe von f(x).
  

• Diese durchschnittliche könnte man als waagrechte Linie eintragen.
  

• Sie ist dann die Länge eines Rechteckes, das von a bis b geht.
  

• Die Höhe des Rechteckes ist der y-Wert dieser Waagrechten Linie.
  

• Die Rechteckfläche ist flächengleich mit der Fläche von f(x) von a bis b.
  

• Das Integral berechnet zunächst die Fläche von f(x) von a bis b.
  

• Dieser Flächeninhalt ist gleich dem der Rechteckfläche.
  

• Von der Rechteckfläche ist die Länge bekannt: b-a.
  

• Man dividiert also die Rechteckfläche durch b-a.
  

• Das Ergebnis ist die gesuchte Rechteckhöhe.
  

• Sie ist gleich dem gesuchten Mittelwert.