Mittelwert von Funktionswerten
Arithmetisches Mittel
© 2016
- 2025
Basiswissen
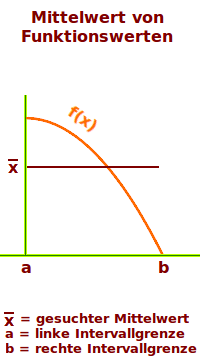
Man hat den Graphen einer Funktion, etwa eine nach unten geöffnete Parabel, wie von der Funktion f(x)-x²+1. Man kann nun alle Funktionswerte (es sind unendlich viele) zwischen zwei Punkten des Graphen betrachten. Wie könnte man ihren Mittelwert, also ihren Durchschnitt berechnen? Eine Lösung ist hier kurz vorgestellt.
Defiition
- Mittelwert meint hier ein 👉 arithmetisches Mittel
- Und zwar: das arithmetische Mittel von Funktionswerten.
- Funktionswerte sind die f(x)- oder y-Werte einer Funktion.
Sachbeispiel
- Man hat zum Beispiel die Funktion: f(x)=-x²+1
- Als Sachaufgabe wäre denkbar: ein Ball wird waagrecht geworfen.
- Der Start der Flugbahn liegt auf der y-Achse bei einer Höhe von 1 Meter.
- Der Ball fliegt nach rechts und folgt dabei dem Graph f(x)=-x²+1.
- Nach einem Meter trifft er bei x=1 auf die x-Achse, hier also den Boden.
- Man kann nun fragen: was war seine durchschnittliche Flughöhe?
- Anders gesagt: was war das arithmetische Mittel der Flughöhe?
- Siehe auch 👉 arithmetisches Mittel
Berechnung
- Die Flughöhe ist der jeweilige f(x)- oder y-Wert.
- Man eschränkt sich auf den Bereich von x=0 bis x=1.
- Man könnte theoretisch alle y-Werte dieses Bereiches aufaddieren.
- Dann teilt man das Ergebnis durch die Anzahl der y-Werte.
- Das Ergebnis wäre das arithmetische Mittel der Flughöhe.
- Problem: man hat unendlich viele y-Werte in dem Bereich.