Lokales Maximum
Definition
© 2016
- 2025
Basiswissen|
Was meint "lokales Maximum"?|
Was wäre ein Beispiel?|
Was wäre kein lokales Maximum?|
Was ist das absolute Maximum?|
Wie bestimmt man ein lokales Maximum rechnerisch?|
Verwandte Konzepte|
Geographie: Dominanz|
Evolution: der Bergsteigeralgorithmus|
Fußnoten
Basiswissen
Der y-Wert oder die Stelle auf der y-Achse, die zu einem lokalen Hochpunkt gehört nennt man ein lokales Minimum. Das ist hier näher erklärt.
Was meint "lokales Maximum"?
- Das Wort bezieht sich auf y-Werte einer Funktion.
- Ein lokales Maximum ist ein y-Wert, dessen direkte Nachbarn kleiner sind.
- Ein lokales Maximum gehört immer zu einem lokalen 👉 Hochpunkt
Was wäre ein Beispiel?
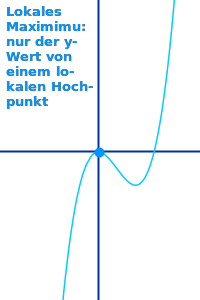
- Betrachte den Graphen von 👉 f(x)=x³-3x
- Links gibt es einen Hochpunkt bei x=-1.
- Der y-Wert von diesem Hochpunkt ist 2.
- Direkt links und rechts davon gibt es keine höheren Werte.
- Direkt links und rechts davon sind nämlich alle y-Werte kleiner.
- So einen lokal maximalen y-Wert nennt man lokales Maximum.
- Der entsprechende x-Wert ist die 👉 lokale Hochstelle
Was wäre kein lokales Maximum?
- Betrachte wieder den Graphen von 👉 f(x)=x³-3x
- Ganz rechts geht der Graph nach oben weg.
- Der Graph verläuft dort oberhalb des Hochpunktes.
- Dort gibt es aber trotzdem keine Hochpunkte.
Was ist das absolute Maximum?
- Der Überhaupt höchste y-Wert eines Graphen heißt absolutes Maximum.
- Es gibt dann tatsächlich keinen größeren y-Wert mehr.
- Das absolute Maximum im Beispiel wäre plus Unendlich.
Wie bestimmt man ein lokales Maximum rechnerisch?
- Dazu gibt es verschiedene Verfahren.
- Es geht graphisch, rechnerisch, über Probieren oder sonstwie.
- Beschrieben ist das unter 👉 Hochpunkte bestimmen
Verwandte Konzepte
Die Grundidee eines lokalen Maximums ist es, dass ein Punkt in seiner unmittelbaren Umgebung keine höheren Konkurrenten hat. Das Wesentliche ist hier dass man sich nur auf die allernächste Umgebung beschränkt. [1] Diese Idee findet sich auch in anderen Zusammenhängen außerhalb der mathematischen Analysis.
Geographie: Dominanz
Bis zu welcher Entferntung dominiert der Gipfel eines Berges seine Umgebung? Anders gefragt: wie weit müsste man von einem Berggipfel aus gehen, bis man zu einem noch höher gelegen Punkt kommt? Siehe mehr zu diesem Konzept im Artikel 👉 Dominanz (Geographie)
Evolution: der Bergsteigeralgorithmus
Das Auffinden lokaler Maxima, also möglichst hoher Bereiche in einer begrenzten Umgebung, wird modellhaft auch auf die Evolution übertragen: wie können Individuen oder Arten in der sogenannten Fitnesslandschaft möglichst zuverlässig immer bergauf hin zu mehr Fitness, hin zu mehr evolutionärer Tauglichkeit, wandern? Eine Lösungsidee sind sogenannte genetische Algorithmen. Eine besonders einfache und leicht verständliche Version davon ist der sogenannte 👉 Bergsteigeralgorithmus
Fußnoten
- [1] In der Mathematik wird die "allernächste Umgebung" eindeutig definiert als sogenannte 👉 Epsilon-Umgebung