Kartesische Form in Exponentialform
Umwandlung
© 2016
- 2025
Basiswissen
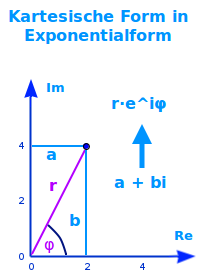
Die kartesische Form a+bi kann umgewandelt werden in die Exponentialform einer komplexen Zahl. Das ist hier kurz erklärt.
Umwandlung
- Kartesische Form: a+bi
- Exponentialform: r·e^(i·phi)
- r = √(a²+b²)
- phi = arcustangens von b durch a
Legende
- r = Betrag der Zahl, Abstand zum Ursprung
- e = Eulersche Zahl, etwa 2,71828
- i = Imaginäre Einheit
- phi = Argument der komplexen Zahl
In Worten
Man hat eine komplexe Zahl in kartesischer Form a+bi. Man berechnet zuerst den Betrag r indem man a²+b² rechnet und aus dem Ergebnis die Wurzel zieht. Dann berechnet man den Winkel phi: man dividiert b durch a und nimmt davon den Arkustangens.
Die Umkehrung
Man kann auch umgekehrt eine Exponentialform umwandeln in die kartesische Form. Das ist erklärt unter Exponentialform in kartesische Form ↗