Grundidee

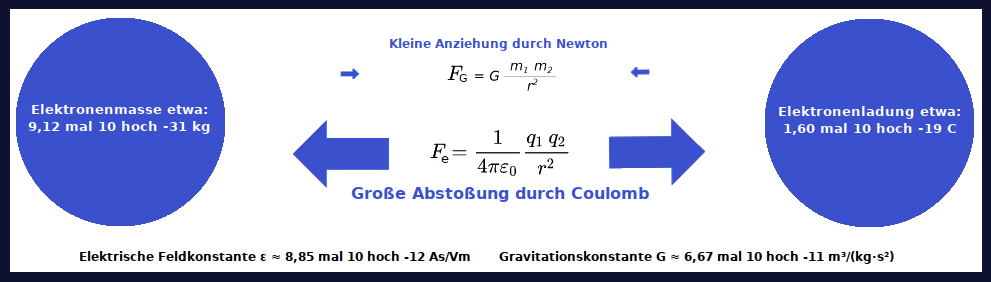
Die Kraft, mit der zwei Elektronen sich gegenseitig abstoßen ist rund 4,17 mal 10 hoch 42 mal so stark wie die Gravitationskraft, mit der sie sich gegenseitig anziehen. Die Zahl gilt unabhängig vom Abstand der zwei Teilchen. Der Physiker Richard Feynman (1918 bis 1988) spekulierte auch über einen tieferen kosmologischen Sinn dieser Verhältniszahl, die wir hier kurz als Feynman-Verhältnis bezeichnen.

Bildbeschreibung und Urheberrecht — Zwei Elektronen ziehen sich mit einer schwachen Gravitationskraft im Sinne Newtons an, stoßen sich aber gleichzeitig mit einer enorm starke elektrostatischen Kraft nach Coulomb ab. Feynman zufolge liegt das Verhältnis bei etwa 4 Septillionen zu 1.☛

Originalzitat

Der Physiker Richard Feynman war bekannt dafür, dass er scheinbar alltägliche Fakten der Physik so verfremdend darstellen konnte, dass daraus interessante Rätsel oder sehr bemerkenswerte Feststellungen wurden. Ein viel zitiertes Beispiel dafür ist, wie er den enorm großen Unterschied zwischen der Stärke der elektrostatischen Kraft und der Gravitationskraft zu einer Ungeheurlichkeit macht.

ZITAT:

Richard Feynman: "Wenn wir in einigen natürlichen Einheiten die Abstoßung zweier Elektronen […] aufgrund von Elektrizität und die Anziehungskraft zweier Elektronen aufgrund ihrer Massen berücksichtigen, können wir das Verhältnis der elektrischen Abstoßung zur gravitativen Anziehung messen. […] Die Gravitationsanziehung im Verhältnis zur elektrischen Abstoßung zwischen zwei Elektronen beträgt 1 geteilt durch 4,17×10^42!

Für zwei Elektronen kann man also sagen, dass die Abstoßung zwischen ihnen gut 4,2 Septillionen mal so stark ist, wie die Anziehung zwischen ihnen. Eine Septillion ist eine 1 mit 7 (sept=sieben) mal 6 Nullen, also 42 Nullen.^[2] Doch Feynman bleibt nicht beim bloßen Konstatieren stehen. Er sucht nach einem tieferen Sinn dieser Zahl.

Ein kosmologischer Sinn?

Naturkonstante

Feynman fragt sich, wo eine solch große Zahl herkommt. Die Zahl sei nicht zufällig (accidental) wie etwa das Verhältnis des Erdvolumens zum Volumen eines Flohs. Feynman spricht ausdrücklich von einer Naturkonstanten. Wo könnte eine so ungeheuerlich (tremendous) große Zahl herkommen, fragt er. Er vermutet, dass sie tief in der Natur (something deep in nature) verwurzelt ist. Er spekuliert, dass man vielleicht eines Tages eine Weltformel (universal equation) finden wird, und diese Zahl eine ihrer Lösungen (roots) ist. Aber er wendet gleich ein, dass es wohl sehr schwer wäre eine Gleichung für eine so phantastisch (fantastic) große Zahl als Lösung zu finden.

Lichtzeiten

Mit einem Ansatz allerdings kommt Feynman zu der gesuchten Zahl 10 hoch 42: er nimmt das grobe Alter des Universums in Jahren und vergleicht es mit der Zeit in Sekunden, die Licht benötigt, den Durchmesser eines Protons zu durchfliegen. Das Universum ist etwa 10 hoch 10 Jahre alt. Die Zeit, die Licht zum durchfliegen eines Protonendurchmesser benötigen würde ist rund 10 hoch -24 Sekunden. Das Zahlenverhältnis berechnet man über 10 hoch 10 geteilt durch 10 hoch -24.

🖩

10¹⁰:10⁻²⁴ geht über die Potenzgesetze. Die Basen sind gleich, man rechnet also Zählerpotenz minus Nennerpotenz, hier also: 10 minus -24 was 10+24 und damit am Ende 42 gibt.

Erdgeschichte

Doch hier wendet Feynman zu Recht ein, dass sich ja das Alter des Universums mit der Zeit verändert. Und wenn die Reisezeit von Licht durch einen Protonendurchmesser gleich bleibt, müsste sich die Konstante mit der Zeit ändern. Mit einem Gedankensprung kommt Feynmann dann zu der Folgerung, dass sich die Gravitationskonstante G mit der Zeit ändern müsste. In der Frühzeit der Erdgeschichte, so Feynman, müsste sie rund 10 % größer gewesen sei als heute. Damit wäre aber auch der Erdorbit näher an der Sonne gewesen als er heute ist. Und infolgedessen wäre das gesamte Wasser auf der Erde nicht flüssig in Ozeanen sondern gasförmig als Dampf in der Atmosphäre gewesen. Da wir aber sichere Sedimentgesteine und Fossilien kennen, die nur in flüssigem Wasser entstehen könnten, muss man diese Spekulation wieder verwerfen.

ZITAT:

Richard Feynman: "Doch solche Argumente sind nicht besonders überzeugend. Das Thema ist noch nicht ganz abgeschlossen."^[3]

Es ist eine Eigenart Feynmans, die Physik nicht als Gebäude fertiger und abgeschlossener Lehrsätze und Theorien zu vermitteln. Es gelingt ihm auf eine spannende Weise, tiefere Ungereimtheiten oder zumindest Auffälligkeiten so zu vermitteln, dass der eigene Forschergeist angefacht wird. Wer mehr davon möchte, dem seien Bücher wie "QED Die Seltsame Theorie des Lichts und der Materie" oder seine legendären Vorlesungen, die Feynman Lectures, empfohlen. Siehe dazu auch die Seite über 👉 Richard Feynman

Fußnoten

[1] "If we take, in some natural units, the repulsion of two electrons (nature’s universal charge) due to electricity, and the attraction of two electrons due to their masses, we can measure the ratio of electrical repulsion to the gravitational attraction. The ratio is independent of the distance and is a fundamental constant of nature. […] The gravitational attraction relative to the electrical repulsion between two electrons is 1 divided by 4.17×10^42!" In: Richard P. Feynman, Robert B. Leighton, Matthew Sands: The Feynman Lectures on Physics, Vol. I. Addison-Wesley, 1963. See Chapter “The Theory of Gravitation”, section on relative force strengths. Online: URL: https://www.feynmanlectures.caltech.edu/I_07.html

[2] Die deutschssprachige Benennung großer Zahlen mit illionen und illiarden folgt einer recht einfachen Logik. Diese ist erklärt im Artikel zur Wortendung 👉 illion

[3] "But such arguments as the one we have just given are not very convincing, and the subject is not completely closed." In: Richard P. Feynman, Robert B. Leighton, Matthew Sands: The Feynman Lectures on Physics, Vol. I. Addison-Wesley, 1963. See Chapter “The Theory of Gravitation”, section on relative force strengths. Online: URL: https://www.feynmanlectures.caltech.edu/I_07.html