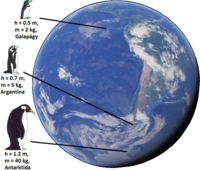
Bergmannsche Regel
🐧Biologie
© 2016
- 2026
Basiswissen|
Ursache|
Pinguine|
Die Bergmannsche Regel als statistische Abhängigkeit|
Die Mathematische Ursache der Bergmannschen Regel|
Wärme oder Temperatur: ein wichtiger Unterschied|
Fußnoten
Basiswissen
Die Bergmannsche Regel beschreibt ursprünglich die Beobachtung, dass bei nahe verwandten Arten gleichwarmer Tiere (homoiothermer Tiere) die durchschnittliche Körpergröße zu den Polen hin ansteigt. Diesen Zusammenhang von durchschnittlicher Körpergröße und Klima beschrieb der Göttinger Anatom und Physiologe Carl Bergmann 1847, daher wird er als Bergmannsche Regel bezeichnet. Körpergröße und Klima sind damit für bestimmte Tieraren voneinander statistisch abhängig.
Ursache
Die Tiere versuche die Körpertemperatur konstant zu halten. Näher an den Polen wird es tendenziell kälter. Die Tiere verlieren also leichter Wärmenergie an die Umwelt. Die Wärme wird im Körperinneren gespeichert (und erzeugt). Sie geht aber nur über die Oberfläche verloren. Je weniger Oberfläche ein Tier im Verhältnis zu seinem Volumen hat, desto kleiner ist der relative Wärmeverlust. Große Körper halten ihre Temperatur länger hoch als ansonsten gleichartige kleine Körper [3]. Siehe auch 👉 Wärmeenergie
Pinguine
- Galápagos-Pinguin Spheniscus mendiculus | 50 cm | 2,2 kg | Äquator
- Humboldt-Pinguin S. humboldti | 65 cm | 4,5 kg | 5 bis 35 Grad südliche Breite
- Magellan-Pinguin S. magellanicus | 70 cm | 4,9 kg | 34 bis 56 Grad südliche Breite
- Königspinguin Aptenodytes patagonica | 95 cm | 15 kg | 50 bis 60 Grad südliche Breite
- Kaiserpinguin A. forsteri | 120 cm | 40 kg | 65 bis 77 Grad südliche Breite
Die Bergmannsche Regel als statistische Abhängigkeit
Mathematisch gesprochen gilt: Der Betrag des Breitengrades des Heimatgebietes und die Körpergröße hängen für Tiere einer Art statistisch voneinander ab: in einer Gruppe polnah beheimateter Tiere gibt es mehr große Individuen als unter einer Gruppe eher äquatornaher Tiere. Weitere Beispiele unter 👉 statistische Abhängigkeiten
Die Mathematische Ursache der Bergmannschen Regel
Eine kleine Kugel hat mehr Oberfläche pro Volumeneinheit. Umgekehrt: je größer eine Kugel ist, desto weniger Oberfläche hat sie pro Volumeneinheit. Und da Wärme zufällig innerhalb eines Körpers wandert, sinkt bei größeren Kugeln die Wahrscheinlichkeit, dass eine bestimmte Menge an Wärme die Oberfläche erreicht und damit das Volumen verlässt. Die Konsequenz daraus ist: bei großen Kugeln bleibt Wärme statistisch gesehen länger im Körper als bei kleinen Kugeln. Und dasselbe gilt für alle Körper die man nur in der Größe aber nicht der Form ändert (Ähnlickeit). Lies mehr zur Mathematik der Bergmannschen Regel unter 👉 Gesetz vom Flächen- und Volumenwachstum
Wärme oder Temperatur: ein wichtiger Unterschied
Wenn wir zwei massive Kugeln aus gleichartigem Eisen betrachten, die eine Kugel groß, die andere klein, und wenn beide Kugeln mit derselben Temperatur von zum Beispiel 80 °C in kalte Luft von zum Beispiel 10 °C gegeben werden, so wird die große Kugel länger höhere Temperaturen haben als die kleine Kugel. Es ist richtig zu sagen, dass die große Kugel ihre Temperatur länger behält als die kleine. Es wäre aber zunächst falsch zu sagen, dass sie ihre Wärme besser behält. Tastäschlich gibt die große Kugel dank ihrer größeren Oberfläche in jeder Sekunde absolut gesehen mehr Energie in Form von Wärme ab (z. B. in Joule gemessen) als die kleine Kugel. Wegen des Gesetzes vom Flächen- und Volumenwachstum gibt die größere Kugel aber in jeder Sekunde einen kleineren Anteil ihrer Wärmeenergie ab als die kleine Kugel. Richtig sind die folgenden Sätze:
- Die große Kugel behält länger eine hohe Temperatur bei.
- Die große Kugel verliert pro Sekunde mehr Energie in Form von Wärme als die kleine Kugel.
- Die große Kugel verliert pro Sekunde einen kleineren Anteil ihrer Enregie in Form von Wärme als die kleine Kugel.
- Siehe auch 👉 Temperatur und Wärme
Fußnoten
- [1] Ueber die Verhältnisse der Wärmeökonomie der Thiere zu ihrer Grösse. In: Göttinger Studien. 1. Abt., 1847, ZDB-ID 514193-x, S. 595–708.
- [2] Blackburn, Tim M.; Gaston, Kevin J.; Loder, Natasha (1999). "Geographic gradients in body size: a clarification of Bergmann's rule". Diversity and Distributions. 5 (4): 165–174. doi:10.1046/j.1472-4642.1999.00046.x. ISSN 1472-4642.
- [3] Bereits Isaac Newton (1642 bis 1727) suchte nach Gründen, warum große Körper ihre Temperatur länger behalten als kleine Körper. Newton schrieb: "Qu. 11. Do not great Bodies conserve their heat the longest, their parts heating one another, and may not great dense and fix'd Bodies, when heated beyond a certain degree, emit Light so copiously, as by the Emission and Re-action of its Light, and the Reflexions and Refractions of its Rays within its Pores to grow still hotter, till it comes to a certain period of heat, such as is that of the Sun?" In: Isaac Newton: OPTICKS: OR, A TREATISE OF THE Reflections, Refractions, Inflections and colours OF LIGHT. The FOURTH EDITION, corrected. By Sir ISAAC NEWTON, Knt. LONDON: Printed for WILLIAM INNYS at the West-End of St. Paul's. MDCCXXX (1730). Dort die Seite 343.