Gibt: -1/x²
x hoch minus eins kann über die Potenzregel abgeleitet werden und gibt dann -1 durch x². Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
Mathematik | Physik | Chemie
Das kleine x ist der Standardbuchstabe für Variablen und Unbekannte. Es hat daneben noch weitere Bedeutungen. => Ganzen Artikel lesen …
Mathematik
Hoch kann einmal bedeuten, dass etwas eine große Höhe hat: Der Eiffelturm in Paris ist 324 Meter hoch. Die zweite Bedeutung bezieht sich auf Potenzen: 2 hoch 3 ist gleich 2·2·2 oder vom Wert her acht. => Ganzen Artikel lesen …
Minus
Abziehen
Drei minus eins gibt zwei: minus heißt, dass man etwas abziehen oder wegnehmen soll. Man soll dann sagen, wie viel danach noch übrig ist. => Ganzen Artikel lesen …
1
Die 1 ist die erste und kleinste natürliche Zahl. Anschaulich steht sie für eine Sache oder oft auch das Ganze. Hier stehen einige Angaben zur Zahl eins. => Ganzen Artikel lesen …
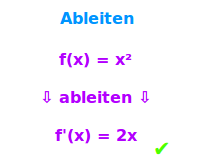Ableiten
Verfahren
Ableiten heißt f'(x) bilden: Ableiten im engeren Sinn heißt: Für einen Funktionsgraphen an einem Punkt die Steigung bestimmen. Im allgemeineren Sinn steht es dafür, die Ableitungsfunktion f'(x) zu bestimmen. Hier sind Regeln zur Bestimmung von f'(x) zusammengestellt. => Ganzen Artikel lesen …
Gibt ln|x|
f(x) = x hoch minus eins kann auch geschreiben werden als f(x)=1/x. Beide Funktionsterme sind äquivalent. Die Aufleitung, als F(x) davon ist: F(x) = ln|x|. Die zwei senkrechten Striche heißen Betragsstriche. Siehe auch => A
gibt: 3x^2
… gibt: 0,5x^(-0,5) oder 0,5/(Wurzel von x)
gibt: 2x
