 Uneigentliches Integral
Uneigentliches Integral
∫f(x)·dx von a bis z über Limes
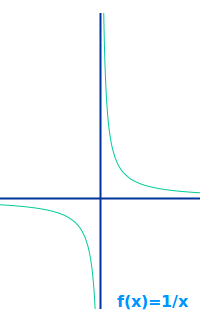
Uneigentlich für ein Integral heißt anschaulich: die dadurch berechnete Fläche hat an einer Stelle einen offenen Rand. Dieser offene Rand wird aber in Richtung der x-Achse oder in Richtung der y-Achse ständig immer enger. Wie man solche Integrale berechnet und wie man den integralwert dann deutet wird hier kurz erklärt. => Ganzen Artikel lesen …
∫: Definition
Das bestimmte Integral ist immer ein einzelner Zahlenwert. Ein unbestimmtes Integral hingegen ist eine Funktion. Neben dieser mathematischen Deutung heißt das Adjektiv integral auch so viel wie der wesentliche Teil von einem größeren Ganzen [1]. Hier wird die mathematische Bedeutung des Wortes Integral erklärt. => Ganzen Artikel lesen …
… siehe unter => uneigentliches Integral
Analysis
Ein eigentliches Integral ist der Zahlenwert, der zu einer rundum vollständig begrenzten Fläche gehört, die von einem Funktionsgraphen, senkrechten Linien an den Intervallgrenzen und einer der beiden Koordinatenachsen gebildet wird. Das Gegenstück dazu ist das => uneigentliches Integral
… Definition unter => uneigentliches Integral
Anleitung
Der Graph einer Funktion nähert sich asymptotisch einer waagrechten Linie immer mehr an. Dadurch entstehen gedacht unendlich lange Flächen parallel zur x-Achse. Der Flächeninhalt kann dennoch oft exakt berechnet werden. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Anleitung
Der Graph einer Funktion nähert sich irgendwo asymptotisch einer senkrechten Linie an. Dadurch entsteht gedanklich ein unendlich langes Flächenstück parallel zur y-Achse. Der Flächeninhalt davon kann dennoch oft exakt berechnet werden. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …

