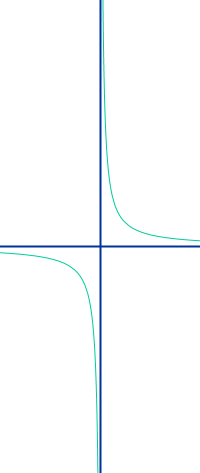
 Umgekehrt proportionale Funktion
Umgekehrt proportionale Funktion
f(x)=a/x
f(x) = a/x ist die allgemeine Form einer umgekehrt proportionalen Funktion. Man spricht auch von einer umgekehrt proportionalen Zuordnung [1] oder einer antiproportionalen Zuordnung. Jede Funktion, die man in diese Form umwandeln kann, ist umgekehrt proportional. Als Funktionsterm hat man eine Zahl geteilt durch x. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Genau andere Reihenfolge
Das Wort „Rot“ ergibt umgekehrt geschrieben „Tor“. Umgekehrt heißt: die Reihenfolge genau andersherum machen. => Ganzen Artikel lesen …
 Funktion
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
Beispiele
Wenn sich der x-Wert verdoppelt, dann halbiert sich der y-Wert: das ist das Erkennungsmerkmal einer umgekehrt proportionalen Funktion. Das ist gleichbedeutend mit der Aussage, dass das Produkt aus x und y immer denselben Wert ergibt, also konstant ist. Der dazugehörige Graph ist eine Hyperbel. Hier stehen einige Beispiele als Gleichungen sowie auch Sachthemen (Hebel, elektrische Spannung, Rechteckflächen etc.). => Ganzen Artikel lesen …
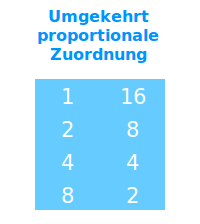 Umgekehrt proportionale Zuordnung
Umgekehrt proportionale Zuordnung
… das Thema steht unter => umgekehrt proportionale Funktion
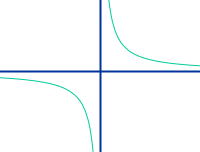 Antiproportionale Funktion
Antiproportionale Funktion
… meint dasselbe wie => umgekehrt proportionale Funktion
Beispiel
f(x) = 40/x oder f(x) = 1/x sind beides Beispiele für eine proportionale Funktion. Sie können nicht direkt über die Potenzregel abgeleitet werden, sie müssen vorher so umgeformt werden, dass das x im Zähler (oben) steht. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => umgekehrt proportionale Gleichung aus Versuch
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen

