Definition
Eine stetige Funktion hat keine Lücken im Definitionsbereich. Es gibt auch keine Sprünge in den y-Werten. Es darf aber Knicke geben. Kleine Änderungen von x ergeben immer auch nur kleine oder keine Änderung von y. Das ist hier kurz noch erläutert. => Ganzen Artikel lesen …
 Funktion
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
… z. B. „an der Stelle Siehe unter => Stellen von Graphen
 Keine Funktion
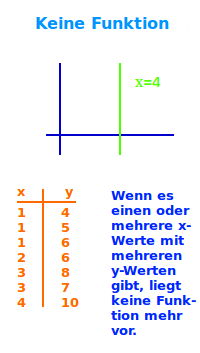
Keine Funktion
Keine eindeutige Zuordnung
Wenn es x-Werte mit mehreren dazugehörigen y-Werten gibt, liegt keine Funktion mehr vor. An einem Graphen erkennt man das daran, dass der Graph an manchen Stellen senkrecht verläuft. => Ganzen Artikel lesen …
… x < 0 gibt 0, alles andere gibt 1 => Heaviside-Funktion
… x < 0 gibt 0, alles andere gibt 1, siehe auch => Heaviside-Funktion
 Sättigungsfunktion
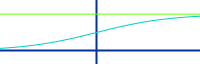
Sättigungsfunktion
Definition
y oder f(x) wächst immer langsamer: mit größer werdendem x-Wert wird auch der dazugehörige y-Wert immer größer. Es gibt aber eine obere Grenze, die dabei nie überschritten wird. Die Wachstumsrate (erste Ableitung) nähert sich für wachsende x-Werte vom Positiven her der Null an. Das wird näher behandelt im Artikel => nach oben beschränktes Wachstum

