Senkrechte Gerade
Begriffsklärung
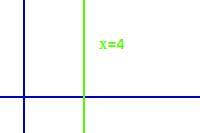
Die Gerade mit der Gleichung x=4 steht senkrecht in einem xy-Koordinatensystem, sie verläuft damit von unten nach oben und ist parallel zur y-Achse. Sie besteht aus allen Punkten, deren x-Koordinate 2 ist. Da zu jedem x-Wert mehr als ein y-gehört ist das keine Funktion sondern eine Zuordnung. Man spricht auch von einer => Ortslinie
Senkrechte
Etwas mit 90°-Winkel
Ein Sendemast ragt zum Beispiel als Senkrechte in den Himmel: eine Gerade, Strecke oder Ebene kann eine Senkrechte zu etwas anderem sein. Das heißt, es gibt einen rechten Winkel (90°). Verschiedene Fälle, die dabei auftreten können sind ausführlicher erklärt in dem Artikel => Orthogonale
Gerade
Übersicht
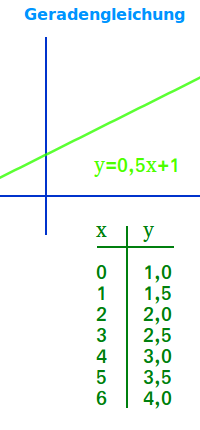
Eine Gerade in der Mathematik ist eine Linie ohne Ecken, Lücken, Kurven oder Enden: sie ist unendlich lang gedacht. Die kürzeste Verbindung zwischen zwei Punkten liegt immer auf einer Geraden. Hier werden Geraden in verschiedenen Teilgebieten der Mathematik kurz vorgestellt. => Ganzen Artikel lesen …
Senkrechte Geraden
Mathematik
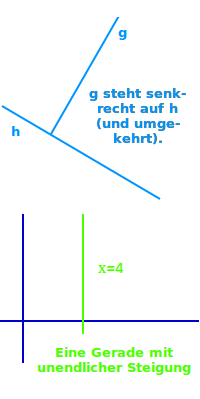
Eine Gerade heißt senrecht, wenn sie mit einem Winkel von 90° auf die Erdoberfläche triffe. Zwei Geraden sind zueinander senkrecht, wenn sie sich mit einem Winkel von 90° schneiden. => Ganzen Artikel lesen …
… ist nicht linear, warum steht unter => senkrechte Gerade
Waagrechte Gerade
Funktionsgraph
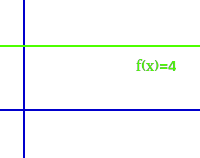
Waagrecht heißt hier: von links nach rechts in einem xy-Koordinatensystem. Damit verläuft die Gerade parallel zur x-Achse. Ein typisches Beispiel ist: f(x)=4 => Ganzen Artikel lesen …
… ungebräuchlich, man spricht von => VTOL
Zueinander senkrechte Geraden
90°-Winkel
Zwei Geraden heißen senkrecht zueinander, wenn sie an ihrem Schnittpunkt einen 90°-Winkel bilden. Hier wird kurz erklärt, wie man solche Geraden bestimmen kann. => Ganzen Artikel lesen …
Schritt-für-Schritt
Für ein xy- und auch ein xyz-Koordinatensystem: hier stehen Anleitung, wie man zu einer gegebenen Geraden eine senkrechte Gerade findet. => Ganzen Artikel lesen …
