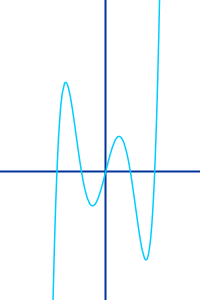
Quintische Funktion
Hoch 5
Die höchste Potenz von x ist die 5: eine quintische Funktion heißt auch ganzrationale Funktion fünften Grades. Ihr Graph ist eine quintische Parabel. Die Funktion ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
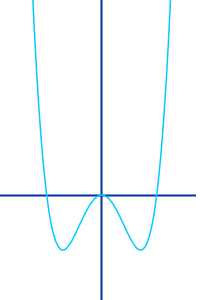Quartische Funktion
f(x)=T(x⁴)
Ganzrationale Funktion mit höchstens x hoch 4: als quartisch bezeichnet man eine Funktion, die man in die Form f(x) = a·x⁴ + b·x³ + c·x^2 + d·x + e bringen kann. Ein anderer, gleichbedeutender Name ist ganzrationale Funktion vierten Grades. Das Wort quartisch steht für 4 und bezeichnet die höchste vorkommende Potenz der unabhängigen Variablen x. => Ganzen Artikel lesen …
Beispiele
Quintisch heißt: ganzrational vom Grad 5. Eine quintische Funktion ist also eine ganzrationale Funktion fünften Grades. Das heißt, die größte Exponent, der von x vorkommt ist die Zahl 5. Es kann, muss aber keine niedrigeren Potenzen von x geben. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
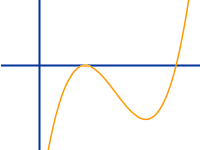Kubische Funktion
x³
Jede Funktion, die man umwandeln kann in die Form f(x) = ax³ + bx² + cx + d heißt kubisch. Das x³ muss mindestens einmal vorkommen. Andere Glieder dürfen, müssen aber nicht vorkommen. Eine kubische Funktion ist immer auch eine ganzrationale Funktion. => Ganzen Artikel lesen …
… z. B. von x^5, siehe unter => Parabel fünfter Ordnung
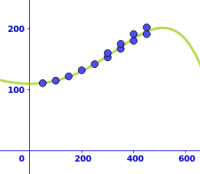Quintische Funktion aus Gummibandversuch
Anleitung
Etwa 10 bis 30 Minuten: der Versuch zeigt zweierlei: wie a) eine ganzrationale Funktion fünften Grades eine Gummibanddehnung modelliert und b) wie die erste Ableitung f'(x) praktisch gedeutet werden kann. => Ganzen Artikel lesen …
