Parallele Vektoren
Erkennen
Zwei Vektoren mit gleicher Richtung oder genau entgegengesetzter Richtung heißen zueinander parallel oder auch kollinear. Man schreibt für zwei zueinander parallele Vektoren a und b auch kurz: a ⇈ b [1]. Die Vektoren dürfen unterschiedlich lang sein, müssen es aber nicht. Sie dürfen - müssen aber nicht - Gegenvektoren zueinander sein. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Eine Gerade, die parallel zu irgendetwas anderem ist
Wenn zwei Geraden parallel zueinander sind, dann haben sie die gleiche Steigung. Die folgenden Gleichungen gehören alle zu parallelen Geraden: => Ganzen Artikel lesen …
⊗☉↗⮅ Arten und Einteilung
Vektoren sind gedachte Pfeile in einem 2D-, 3D- oder höherem Koordinatensystem. Sie werden oft aus zwei oder drei Zahlen zusammengesetzt, etwa (4|3|5). => Ganzen Artikel lesen …
… unterscheiden sich nur um positives Vielfaches => parallele Vektoren
… für verschiedene Objekte, siehe unter => nicht parallel
… ein Vektor kann parallel sein zu anderen Vektoren (oder Ebenen), mehr unter => parallele Vektoren
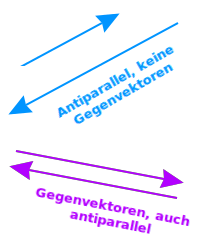
Antiparallele Vektoren
⮂ Definition
⮂ Ein Vektor ist das (skalare) negative Vielfache des anderen Vektors: beide Vektoren sind damit auch parallel, sie zeigen mit ihren Pfeilspitzen aber in entgegengesetzte Richtung. [1]. Antiparallele Vektoren sind ein Sonderfall kollinearer Vektoren. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… unterscheiden sich nur um positives Vielfaches => parallele Vektoren
… für verschiedene Objekte, siehe unter => nicht parallel
