 Parallel
Parallel
Definition
Parallel heißt: der kürzeste Abstand zweier Objekte ist überall gleich groß. Man spricht zum Beispiel von parallelen Linien, Geraden oder Flächen. Das wird hier erläutert. => Ganzen Artikel lesen …
Eine Gerade, die parallel zu irgendetwas anderem ist
Wenn zwei Geraden parallel zueinander sind, dann haben sie die gleiche Steigung. Die folgenden Gleichungen gehören alle zu parallelen Geraden: => Ganzen Artikel lesen …
 Parabel
Parabel
Analysis
In der Schulmathematik ist die Parabel meist der Graph einer quadratischen Funktion, z. B. von f(x)=x²+2) [1]. Daneben gibt es aber noch weitere Bedeutungen [2], die hier auch kurz vorgestellt werden. => Ganzen Artikel lesen …
Tier
Als Koralle bezeichnet man ein Nesseltier, das ortsfest (sessil) in Kolonien lebt. Korallen können - müssen aber nicht - Riffe bilden. Diese Nesseltiere (Cnidaria) sind aber biologisch nicht näher miteinander verwandt. Siehe als Beispiel auch => Steinkoralle
… für verschiedene Objekte, siehe unter => nicht parallel
… siehe unter => parallel
Geometrie
Parallelogrammprisma oder Parallelepiped: diese beiden Körper haben Parallelogramme als Begrenzungsflächen und passen am ehesten auf die Idee eines 3D-Parallelogramms. Beide sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… heißt in der Mathematik => Parallelogramm
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… zur Erkennung siehe unter => ähnliche Dreiecke über Matroschka-Methode
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
Vektoren
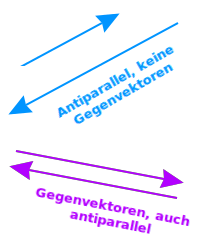
Antiparallele Vektoren sind parallel zueinander. Sie zeigen jedoch mit ihrer Pfeilspitze in genau entgegengesetzte Richtung. Das Präfix Anti heißt so viel wie „gegen“ (antisozial, Antiteilchen). Vektoren, nicht aber Punkte, Geraden oder Ebenen können antiparallel sein. Wenn zwei antiparallele Vektoren auch gleich lang sind, dann sind sie auch sogenannte Gegenvektoren. Mehr dazu unter => antiparallele Vektoren
Unklare Begriffshierarchie
In der Vektorrechnung werden die Begriffe parallel und antiparallel im Bezug auf Vektoren gebraucht. Antiparallel wird dabei so verwendet, dass die Vektoren parallel zueinander verlaufen, ihre Pfeilspitzen aber in entgegengesetzte Richtungen zeigen. Das erzeugt widersprüchliche Bedeutungen der Vorsilbe anti, was hier kurz erklärt wird. => Ganzen Artikel lesen …
… für verschiedene Objekte, siehe unter => nicht parallel
 Antiparallele Vektoren
Antiparallele Vektoren
⮂ Definition
⮂ Ein Vektor ist das (skalare) negative Vielfache des anderen Vektors: beide Vektoren sind damit auch parallel, sie zeigen mit ihren Pfeilspitzen aber in entgegengesetzte Richtung. [1]. Antiparallele Vektoren sind ein Sonderfall kollinearer Vektoren. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… unterscheiden sich nur um negatives Vielfaches => antiparallele Vektoren
… unterscheiden sich nur um negatives Vielfaches => antiparallele Vektoren
… unterscheiden sich nur um negatives Vielfaches => antiparallele Vektoren
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… von einer Ecke zur anderen, mehr unter => Parallelogrammdiagonale
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
Parallel aber nicht identisch
Zwei Geraden sind parallel, wenn sie überall genau denselben Abstand haben. Sie können dabei auch identisch sein, also überall den Abstand 0 haben. Möchte man sagen, dass sie parallel sind, aber tatsächlich nicht dieselben Geraden sind, dann sagt man: sie sind parallel aber nicht identisch. Verkürzt nennt man das auch „echt parallel“. => Ganzen Artikel lesen …
Parallel aber nicht identisch
Zwei Geraden sind parallel, wenn sie überall genau denselben Abstand haben. Sie können dabei auch identisch sein, also überall den Abstand 0 haben. Möchte man sagen, dass sie parallel sind, aber tatsächlich nicht dieselben Geraden sind, dann sagt man: sie sind parallel aber nicht identisch. Verkürzt nennt man das auch „echt parallel“. => Ganzen Artikel lesen …

