3D-Geraden
Zwei Geraden in einem xy-Koordinatensystem stehen orthogonal zueinander, wenn sie in ihrem Schnittpunkt einen 90°-Winkel bilden. Zwei Geraden in einem xyz-Koordinatensystem stehen orthogonal zueinander, wenn das Skalarprodukt ihrer Richtungsvektoren 0 ergibt. Beide Fälle sind hier kurz erklärt. => Ganzen Artikel lesen …
Etwas mit 90°-Winkel
Eine Gerade, Strecke oder Ebene kann eine Orthogonale zu etwas anderem sein. Das meint dann, dass sie mit einem 90°-Winkel (also senkrecht) auf etwas anderes trifft. Eine Gerade kann zum Beispiele eine Orthogonale von einer anderen Geraden sein. Man unterscheidet dabei 2D- und 3D-Koordinatensysteme. => Ganzen Artikel lesen …
Geraden
In der Mathematik: Klassifizierung und Arten
In der Mathematik werden Geraden sowohl innerhalb der Geometrie (2D und 3D) als auch in der Funktionen- und Gleichungslehre behandelt. In der Anylsis spielen sie als Veranschaulichung von linearen Funktionen (Geradengleichung) eine grundlegende Rolle. Es folgen jetzt verschiedene Typen von Geraden. => Ganzen Artikel lesen …
Vektorrechnung
Zwei Ebenen sind genau dann orthogonal zueinander, wenn ihre Normalnvektoren zueinander orthogonal sind. Ob die zwei Normalenvektoren zueinander senkrecht sind kann man mit Hilfe des Skalarproduktes überprüfen (muss Null ergeben). Mehr zum Hintergrund, siehe unter => Normalenform der Ebene
Orthogonales Trapez
Mindestens ein 90°-Winkel
Ein Trapez ist ein Viereck mit mindestens zwei parallelen Seiten. Die Seiten dürfen - müssen aber nicht - senkrecht aufeinander stehen. Senkrecht aufeinander heißt: mit einem 90°-Winkel. Gibt es in dem Trapez mindestens einen 90°-Winkel, heißt das Trapez auch rechtwinklig oder orthogonal. Siehe allgemein auch => Trapez
Matrizen
Alle nxn (quadratisch) Matrizen für die die folgenden Bedingungen gelten bilden gemeinsam eine orthogonale Gruppe: A⁻¹=Aᵀ und AAᵀ = AᵀA. Ferner gilt noch dass die Determinante von A den Wert 1 hat. Aᵀ die zu A transonierte Matrix. Und A⁻¹ ist die zu A inverse Matrix. Siehe auch => Matrizenrechnung
… „Senkrechtaufeinanderheit“, siehe unter => orthogonale Geraden
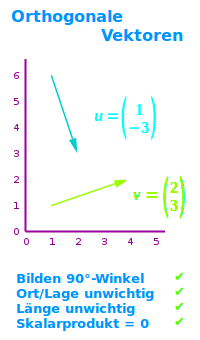
Orthogonale Vektoren
90°-Winkel
Orthogonale Vektoren sind hier zwei oder mehr Vektoren, die zueinander orthogonal, das heißt rechtwinklich sind, also einen 90°-Winkel einschließen. Das Skalarprodukt solcher zueinander orthogonaler Vektoren ist immer 0. => Ganzen Artikel lesen …
… ist nicht linear, warum steht unter => senkrechte Gerade
… 90°-Winkel zwische den Geraden => orthogonale Geraden
