Momentane Änderungsrate
Mathematik
Ein Flugzeug ist im Steigflug. Wenn es in jeder Sekunde einen Meter mehr an Höhe gewinnt, dann ist ein Meter pro Sekunde die momentane Änderungsrate der Höhe des Flugzeuges. Hier wird erklärt, was die momentane Änderungsrate bedeutet und wie man sie berechnet. => Ganzen Artikel lesen …
Änderungsrate
Delta y durch Delta x
Eine Rate in der Mathematik ist immer eine Änderung mit der Zeit. Eine Änderungsrate gibt ein Mehr- oder Wenigerwerden im Bezug auf eine feste Zeiteinheit, etwa: Millimeter pro Jahr oder Euro pro Tag. => Ganzen Artikel lesen …
Definition
Lokal heißt in der Mathematik so viel wie: an einem Punkt oder Ort, nicht ausgedehnt. Eine Rate ist immer eine Änderung pro Zeit. Die lokale Änderungsrate meint damit dasselbe wie die => momentane Änderungsrate
… im Gegensatz zu einer lokalen Änderungsrate, heißt => mittlere Änderungsrate
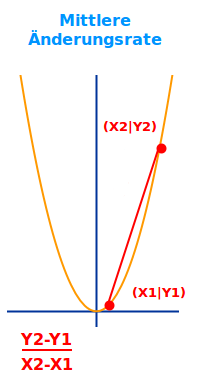Mittlere Änderungsrate
Definition
Die durchschnittliche oder mittlere Änderungsrate gibt an, wie stark sich etwas in einer Sekunde ändern, wenn die Geschwindigkeit der Änderung immer gleich groß wäre. Am Graphen entspricht die mittlere Änderungsrate immer auch der Sekantensteigung. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Mathematik
Man hat ein Weg-Zeit-Diagramm, auch Strecke-Zeit-Diagramm genannt. Die Strecke entspricht dem y-Wert, die Zeit dem x-Wert. Die Ableitung im Sinne der Analysis gibt allgemein die momentane Änderungsrate. Geht es um Strecken und Zeiten, dann ist diese momentane Änderungsrate identisch mit der => Momentangeschwindigkeit
Erste Ableitung
Hat man eine Funktion s(t), also eine zurückgelegte Strecke abhängig von der dafür benötigen Zeit, spricht man auch von einer Weg-Zeit-Funktion oder graphisch von einem Weg-Zeit-Diagramm. Die erste Ableitung einer solchen Funktion gibt die momentane Geschwindigkeit zum Zeitpunkt t, kurz die => Momentangeschwindigkeit
