 Linksseitiger Grenzwert
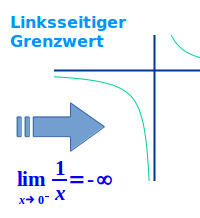
Linksseitiger Grenzwert
Von links kommend
Der Graph der Funktion f(x)=1:x heißt Normalhyperbel. Der Graph geht durch den Punkt (-1|-1). Wenn man dort den Finger gedanklich auf den Graphen legt, kann man den Finger auf dem Graphen nach rechts bewegen. Dabei bewegt man sich von links kommend auf die y-Achse zu. Je näher man an die y-Achse herankommt, desto steiler und tiefer geht der Graph nach unten Richtung minus unendlich. Geht man also von links komment auf x=0 zu (die y-Achse), dann geht der y-Wert gegen minus unendlich. Man sagt: der linksseitige Grenzwert von f(x) für x gegen 0 ist minus unendlich. => Ganzen Artikel lesen …
 Grenzwert
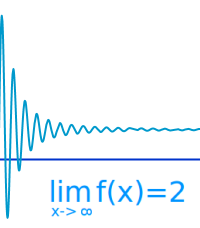
Grenzwert
Analysis
Von einem Grenzwert [1] oder Limes [7] spricht man bei Folgen, Reihen und Funktionen. Hier wird erklärt, wie der Grenzwert im Sinne der Mathematik exakt definiert ist. => Ganzen Artikel lesen …
Funktionen
Man hat den Grahphen einer Funktion f(x). Nähert man sich mit den x-Werten langsam einem ganz bestimmten festgelegten x-Wert von links her an, dann entsteht ein sogenannten linksseitiger Grenzwert. Der linksseitige Grenzwert ist der y-Wert an den man immer besser herankommt. Analog gibt es auch einen rechtsseitigen Grenzwert. Siehe als Beispiel unter => linksseitiger Grenzwert
 Linksseitiger Grenzwert
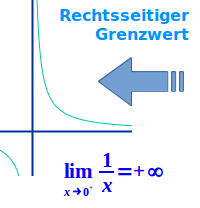
Linksseitiger Grenzwert
Von rechts kommend
Der Graph der Funktion f(x)=1:x heißt Normalhyperbel. Der Graph geht zum Beispiel durch den Punkt (2|0,5). Wenn man dort den Finger gedanklich auf den Graphen legt, kann man den Finger auf dem Graphen nach links abfahren. Dabei bewegt man sich von rechts kommend auf die y-Achse zu. Je näher man an die y-Achse herankommt, desto steiler und höher geht der Graph nach oben Richtung unendlich. Geht man also von rechts komment auf x=0 zu (die y-Achse), dann geht der y-Wert gegen plus unendlich. Man sagt: der rechtsseitige Grenzwert von f(x) für x gegen 0 ist plus unendlich. => Ganzen Artikel lesen …
… Limes, siehe unter => Grenzwert (Funktion)
Auf der linken Seite
Auf der linken Seiten von etwas: in der Mathematik kommt der Begriff in Verbindung mit Grenzwerten (Analysis) und Hypothesentests (Stochastik) vor. Das wird hier kurz vorgestellt. => Ganzen Artikel lesen …

