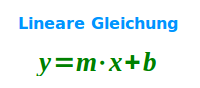 Lineare Gleichung
Lineare Gleichung
Definition
Jede Gleichung, die man umformen kann in y = m·x+b nennt man linear. Wichtig ist, dass das x keine Hochzahl (außer der gedachten 1) hat und auch nicht in einem Nenner steht. Das ist hier näher erklärt. => Ganzen Artikel lesen …
 Gleichung
Gleichung
Definition
4x+5 = 41: Alle Terme zwischen denen ein mathematisches Gleichzeichen steht heißen Gleichung. Das Gleichzeichen besagt, dass links und rechts am Ende der gleiche Zahlenwert stehen sollte, aber nicht stehen muss. Das wird hier näher erklärt. => Ganzen Artikel lesen …
Beispiele
4x = 20-x: hier stehen einige Beispiele und Gegenbeispiele zu linearen Gleichungen. Lineare Gleichungen können eine oder auch mehrere Unbekannte haben. => Ganzen Artikel lesen …
… Beispiele, was das ist => Lineare Gleichungen
… mit f, g und b, siehe unter => Linsenformel
… siehe unter => Altersrätsel ueber x
4 = 2·x
12 = 2·x + 4 ist eine einfache lineare Gleichung. Es kommen keine Brüche ode negativen Zahlen vor. Solche Gleichungen kann man oft schnell durch Einsetzen, also Probieren lösen. Weitere Beispiele stehen unter => einfache lineare Gleichungen
Warum y+2x=10 eine Gerade ergibt
Als Gleichungen im engeren Sinn bezeichnet man Aussagen mit einem Gleichzeichen und einer oder mehreren Unbekannten. y=2x=10 ist eine solche Gleichung. Sie heißt linear, weil die Unbekannten x und y nur über die Punkt- und Strichrechnung verbunden sind. Jedes Paar von x-y-Zahlenwerten, das die Gleichung aufgehen lässt, heißt Lösung dieser Gleichung. Es gibt unendlich viele Lösungen. Hier einige Lösungen: => Ganzen Artikel lesen …
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
… siehe unter => Gerade als geometrischer Ort
… siehe unter => Altersrätsel ueber x
… siehe unter => Geradengleichung aufstellen [meint dasselbe]
… z. B. y = 4x+3 aufstellen => Geradengleichung aus zwei Punkten
Aufgaben mit ganzen kurzen Texten ohne Sachinformation
Beispiel: Das Dreifache einer Zahl vermindert um ihre Hälfte soll 20 ergeben. Dies wäre als Gleichung 3x-0,5x=20. => Ganzen Artikel lesen …
… Kurztipps und Aufgaben, siehe unter => Geradengleichung aus Text
 Lineare Gleichung aus Versuch
Lineare Gleichung aus Versuch
… siehe unter => Geradengleichung aus Versuch
… z. B. y = 4x+3 aufstellen => Geradengleichung aus zwei Punkten
Verfahren
8=2x+2 hat die Lösung x=3. Eine lineare Gleichung kann eine oder zwei Unbekannte haben. Für beide Fälle gibt es eigene Lösungsverfahren, die hier kurz vorgestellt sind. => Ganzen Artikel lesen …
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
x+y=10
x+y=10 hat als Lösung zum Beispiel x=7 und y=3. Eine andere Lösung ist x=9 und y=1. Diese Gleichung hier hat zwei Unbekannte und unendliche viele Lösungen. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
… siehe unter => Geradengleichung aufstellen
Anleitung
4x+18 = 2x+30 hat die Lösung x=6. Hier steht eine Schritt-für-Schritt Anleitung mit Praxisaufgaben im Übungsteil (qck). => Ganzen Artikel lesen …
z. B. 4·(x-5) = 12
Der erste Schritt ist meistens das Auflösen der Klammer. Im Beispiel oben ergäbe das 4x-20 = 12. Dann kann man weiter nach x umformen (ergäbe hier: x=8). Mehr dazu unter => lineare Gleichungen mit Klammern lösen
Beispiel
z. B. 4(2x+3)-8=28 kann zuerst über das Auflösen der Klammer vereinfacht werden. Anschließend kann die Gleichung durch Zusammenfassen und Umformen gelöst werden. Das ist hier Schritt-für-Schritt vorgestellt. => Ganzen Artikel lesen …
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
Bedeutung
y+x=10 ist eine lineare Gleichung mit zwei Unbekannten. Eine Lösung ist zum Beispiel das Zahlenpaar x=9 und y=1. Daneben gibt es noch unendlich viele weitere Lösungen. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
… siehe unter => LGS mit drei Gleichungen
… siehe unter => LGS mit drei Gleichungen
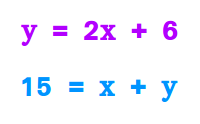 Lineare Gleichungssysteme
Lineare Gleichungssysteme
Arten, Beispiele, Berechnung
Als lineares Gleichungssystem bezeichnet man zwei oder mehr lineare Gleichungen für die man eine gemeinsame Lösung sucht. Die übliche Abkürzung ist LGS. Hier folgen Beispiele unter Typen. Lösungsverfahren (einsetzen, gleichsetzen, addieren, Gauß-Algorithmus) stehen auf => LGS lösen

