Anleitung
f(x)=4x+5 wird abgeleitet zu f'(x)=4: als linear bezeichnet man jede Funktion, die man in die Form f(x)=mx+b bringen kann. Der Graph ist eine Gerade, die an allen x-Stellen dieselbe Steigung hat. Damit muss auch die Ableitungsfunktion für alle x-Werte denselben Funktionswert (nämlich die Steigung von f(x) - haben. Die Ableitung von f(x) ergibt deshalb immer eine konstante Funktion, also f'(x)=Zahl, wobei die Zahl die Steigung von f(x) ist. Siehe auch => Geradensteigung
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
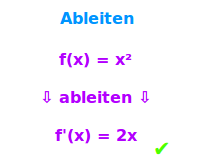Ableiten
Verfahren
Ableiten heißt f'(x) bilden: Ableiten im engeren Sinn heißt: Für einen Funktionsgraphen an einem Punkt die Steigung bestimmen. Im allgemeineren Sinn steht es dafür, die Ableitungsfunktion f'(x) zu bestimmen. Hier sind Regeln zur Bestimmung von f'(x) zusammengestellt. => Ganzen Artikel lesen …
… z. B. y=4x+8 aus Graph bestimmen => Geradengleichung aus Graph
… f(x) = ax+b wird zu F(x) = ½·ax²+bx, mehr unter => Aufleitungsregeln
… z. B. y=4x+8 aus Graph bestimmen => Geradengleichung aus Graph
