Imaginäre Zahl
Z. B. 0+4i oder 2i oder nur i
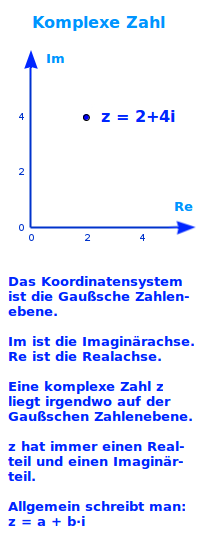
Eine imaginäre Zahl ist immer das Produkt aus einer reellen Zahl b und der imaginären Einheit i. Beispiel: 4i oder -0,025i wären beides imaginäre Zahlen. In der Gaußschen Zahlenebene liegt eine imaginäre Zahl immer auf der y-Achse (Realteil ist 0 [1]). Und das Quadrat einer Imaginären Zahl ergibt immer eine negative reelle Zahl [2]. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Zahl
Mathematik
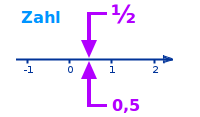
Eine Zahl ist ein Begriff, das heißt eine Vorstellung, von einem Wie-Viel oder Wie-Vielen. Die Zahl selbst ist etwas anderes als ihre Darstellung. Jeder eigene Punkt auf der Zahlengerden ist eine eigene Zahl. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Imaginäre Zahl i
i mal i = -1
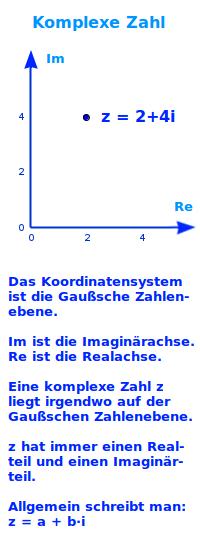
Ist ist die imaginäre Zahl, deren Quadrat genau die reelle Zahl -1 ergibt. Es gilt also: i²=-1. Eine imaginäre Zahl ist eine komplexe Zahl ohne Realteil genau 0 ist. Das Quadrat solcher komplexer Zahlen ist immer eine reelle Zahl. Siehe auch => imaginäre Zahl
… so etwas wie 101001, siehe unter => Binärzahl
Imaginärteil
Von 3+4i wäre: 4i
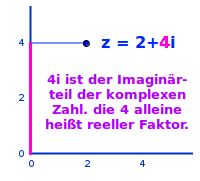
Imaginärteil bezieht sich hier auf eine komplexe Zahl. Eine komplexe Zahl z hat immer einen Realteil a und einen Imaginärteil b·i oder kurz bi. Das kleine b ist dabei immer eine reelle Zahl. Sie heißt Reeller Faktor. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Vorgestellt
Imaginär heißt zunächst so viel wie einbildet [1], erdacht oder ersonnen [2]. Der Gewinn einer Firma ist solange bloß imaginär, wie er noch reines Wunschdenken ist und sich in der Wirklichkeit noch nicht eingestellt hat. In der Mathematik bezeichnet man Zahlen als imaginär, die auch abseits der Zahlengeraden liegen können, deren Realteil genau 0 ist [8], insbesondere die Wurzel aus einer negativen Zahl [9]. Siehe auch => imaginäre Zahl
… ist Siehe unter => i hoch zwei
… ist Siehe unter => i hoch zwei
