A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Imaginäre Zahl

Z. B. 0+4i oder 2i oder nur i

© 2016 - 2025


Basiswissen｜ Wie ist eine imaginäre Zahl formal definiert?｜ Was ist eine imaginäre Zahl anschaulich?｜ Welche Eigenschaften haben imaginäre Zahlen?｜ Fußnoten


Basiswissen


Eine imaginäre Zahl ist immer das Produkt aus einer reellen Zahl b und der imaginären Einheit i. Beispiel: 4i oder -0,025i wären beides imaginäre Zahlen. In der Gaußschen Zahlenebene liegt eine imaginäre Zahl immer auf der y-Achse (Realteil ist 0[1]). Und das Quadrat einer Imaginären Zahl ergibt immer eine negative reelle Zahl[2]. Das ist hier kurz vorgestellt.



Bildbeschreibung und Urheberrecht
Man sieht eine Gaußsche Zahlenebene.☛


Wie ist eine imaginäre Zahl formal definiert?


  • Eine imaginäre Zahl ist immer ein Sonderfall einer komplexen Zahl.
  • Eine komplexe Zahl besteht aus einem Realteil a und einem Imaginärteil bi.
  • Eine imaginäre Zahl ist dann eine komplexe Zahl ohne Realteil a.
  • Es ist also nur der Imaginärteil b·i oder kurz: bi
  • b nennt man auch den reellen Faktor.

Was ist eine imaginäre Zahl anschaulich?


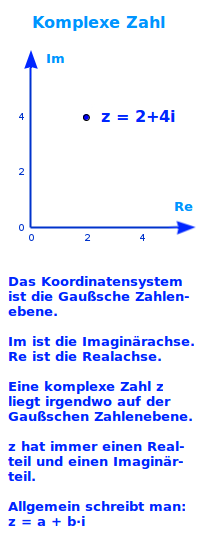
  • Komplexe Zahlen stellt man sich anschaulich in einem xy-Koordinatensystem vor.
  • Dieses Koordinatensystem nennt man die Gaußsche Zahlenebene.
  • Die x-Achse heißt hier Re-Achse und die Im-Achse oder kurz i-Achse.
  • Eine imaginäre Zahl ist dann eine Zahl auf der i-Achse.

Welche Eigenschaften haben imaginäre Zahlen?


  • In der Gaußschen Ebene liegen sie immer auf der Imaginärachse i, ihr Realteil ist also 0[1].
  • Ein imaginäre Zahl zum Quadrat ergibt immer eine reelle Zahl[2].
  • Die relle Zahl kann dabei positiv oder auch negativ sein.
  • Beispiel: (0+i)² = (0+i)·(0+i) = 0²+0i+i0+i² = i² = -1.
  • Die -1 ist eine reelle Zahl.

Fußnoten


  • [1] Realteil ist null: "Imaginäre Zahl eine komplexe Zahl, deren Realteil gleich Null ist." In: Guido Walz: Spektrum Lexikon der Mathematik. Band 2: Eig bis Inn; 2001; ISBN: 3-8274-0437-7. Dort der Artikel "Imaginäre Zahl".
  • [2] Wurzel aus negativer Zahl: "Eine (rein) imaginäre Zahl (auch Imaginärzahl, lat. numerus imaginarius) ist eine komplexe Zahl, deren Quadrat eine nichtpositive reelle Zahl ist." In: Imaginäre Zahl. Wikipedia. Abgerufen am 10. November 2023. Online: https://de.wikipedia.org/wiki/Imaginäre_Zahl