Abgrenzung von exponentiell und Exponential
Mit konstanten Wachstumsfaktor. Kurz erklärt wird der Unterschied zwischen den Worten expoentiell und exponential. => Ganzen Artikel lesen …
… in der Mathematik gleichbedeutend mit => exponentiell
… z. B. 4 hoch 0 oder -3 hoch 0, siehe unter => hoch Null
Beispiele
Der Ausdruck 2 hoch 3 (kurz: 2³) heißt als ganzes Potenz. Die 2 ist die Basis, die 3 ist der Exponent. Der Exponent wird oft klein rechts oberhalb der Basis geschrieben und heißt deshalb auch Hochzahl. Hier stehen noch einige Beispiele. => Ganzen Artikel lesen …
… siehe unter => Potential
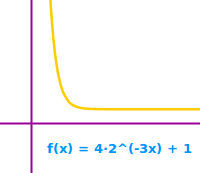 Exponentielle Abklingfunktion
Exponentielle Abklingfunktion
Mathematik
f(x) = a·b^(-k·x+c) + R: der Graph dieser Funktion fällt erst steil ab, flacht dann von links nach rechts gehend stark ab und wird niemals den Funktionswert 5 unterschreiten. Das ist hier allgemein erklärt. => Ganzen Artikel lesen …
 Exponentielle Abnahme
Exponentielle Abnahme
Anschaulich
Als exponentiell bezeichnet man einen Veränderungsprozess, bei dem von einem Schritt bis zum nächten ein Bestand mit immer demselben (Wachstums)Faktor zwischen 0 und 1 multipliziert wird: 32 ⭢ mal 0,5 ⭢ 16 mal 0,5 ⭢ 8 ⭢ mal 0,5 ⭢ 4 ⭢ mal 0,5 ⭢ 2 und so weiter. Das wird hier erklärt. => Ganzen Artikel lesen …
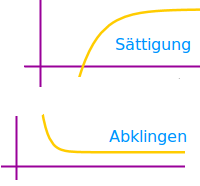 Exponentielle Annäherung
Exponentielle Annäherung
Definition
Wenn x größer wird, gehen die Funktionswert immer näher an einen oberen Maximal- oder unteren Minimalwert heran. Praktische Beispiele sind etwa die betriebswirtschaftliche Marktsättigung (oben) oder die Abkühlung von einem Teeglas (unten). Beides ist hier kurz mathematisch benannt. => Ganzen Artikel lesen …
… x steht als Exponent => Exponentialgleichung
… siehe unter => Allgemeine Exponentialgleichung
… siehe unter => Erweiterte Exponentialgleichung
… siehe unter => Exponentialgleichungen
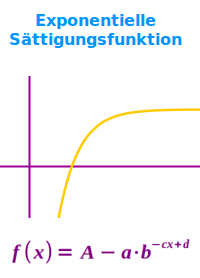 Exponentielle Sättigungsfunktion
Exponentielle Sättigungsfunktion
Definition
f(x) = 4 - 2^(-x + 5): der Graph dieser Funktion steigt erst steil an, flacht dann von links nach rechts gehend stark ab und wird niemals den Funktionswert 4 übersteigen. Das ist hier allgemein erklärt. => Ganzen Artikel lesen …
… Zinsen bleiben auf dem Konto und geben deshalb => Zinseszinsen
… Wachstumsfaktor ist konstant, mehr unter => Exponentielles Wachstum
 Exponentielle Wachstumsprozesse
Exponentielle Wachstumsprozesse
Sachbeispiele
Etwas wächst erst langsam und dann immer schneller oder etwas nimmt erst stark und dann immer langsamer ab: beides bezeichnet eine exponentielle Änderung. Mathematisch fasst man beides oft als exponentielles Wachstum zusammen. Hier stehen einige Beispiele zu Sachthemen. => Ganzen Artikel lesen …
… siehe unter => Exponentielles Wachstum
… B(t) = A·e^(-k·t) + R => exponentielle Abklingfunktion
… siehe unter => System von Exponentialgleichungen
… Übersicht unter => Wachstumsmodelle
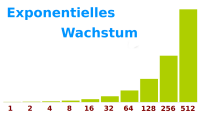 Exponentielles Wachstum
Exponentielles Wachstum
Definition
1 ⭢ 2 ⭢ 4 ⭢ 8 ⭢ 16 ⭢ 32 ⭢ 64 - von einem Schritt zum nächsten Schritt rechnet man immer mit derselben Zahl mal. Hier im Beispiel rechnet man: alter Wert mal zwei gibt den nächsten Wert in der Reihenfolge. Ein solches Wachstum nennt man exponentiell. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… siehe => System von Exponentialgleichungen
… Übersicht unter => Wachstumsmodelle
… siehe => System von Exponentialgleichungen
… Übersicht unter => Wachstumsmodelle
… Übersicht unter => Wachstumsmodelle
… Übersicht unter => Wachstumsmodelle
… Wachstumsfaktor ist konstant, mehr unter => Exponentielles Wachstum

