Einfache logistische Funktion
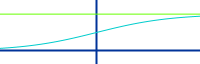
f(x)=1/[1+e^(-x)]
Mit typischer Sättigungskurve: die einfache oder auch elementare logistische Funktion ist die Funktion mit dem einfachstmöglichen Bauplan für einen entsprechenden Graphen. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Einmal irgendwas
Das Einfache von 4 ist 4: das Einfache heißt, dass man etwas genau 1 mal hat. Das Wort ist ähnlich wie das Doppelte oder das Dreifache. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
…)=1/[1+e^(-x)], siehe unter => Einfache logistische Funktion
… nähert sich x-Achse, siehe unter => f(x)=1:(1+e^x)
… f(x)=Siehe unter => Kubische Normalparabel
Logistische Funktion
Wachstum
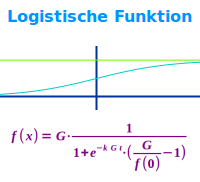
Eine Funktion der Form f(x) = G/[1+(e^(-kGx))·(G/f(0)-1)]: die logistische Funktion hat im xy-Koordinatensystem eine obere und untere Schranke (Begrenzung). Dazwischen steigt oder fällt sie kurzzeitig an. Sie verhindert den Fehler vieler exponentieller Modelle, dass das Wachstum unbebegrenzt ist. => Ganzen Artikel lesen …
für x-Werte von -10 bis 10 zeigt sich deutlich der „Schwanenhals“
Die logistische Funktion gehört zu den Sigmoidfunktionen. Sigmoidfunktionen haben ihren Namen von der Tatsache, dass ihre Graphen ein ein quergelegtes S (Sigma) oder einen Schwanenhals erinnern: Die Graphen nähern sich für x gegen minus unendllich einer unteren Zahl an (hier der 0) und für x gegen unendlich einer oberen Zahl (hier 1). Das kann man gut an der Wertetabelle unten erkennen. Der Wendepunkt liegt bei (0|0,5). => Ganzen Artikel lesen …
