Logistische Funktion
Wachstum
Basiswissen
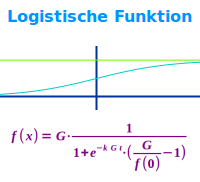
Eine Funktion der Form f(x) = G/[1+(e^(-kGx))·(G/f(0)-1)]: die logistische Funktion hat im xy-Koordinatensystem eine obere und untere Schranke (Begrenzung). Dazwischen steigt oder fällt sie kurzzeitig an. Sie verhindert den Fehler vieler exponentieller Modelle, dass das Wachstum unbebegrenzt ist.
Was bedeuten die Variablen?
- f(x) ist der Funktionswert, oft ein Bestand an Dingen.
- f(x) ist der Funktionswert für x=0, also der y-Achsenabschnitt ↗
- G ist der Sättigungswert, über den der Bestand nicht hinauswächst.
- k ist eine Konstante, die auf den Sachzusammenhang passen muss.
- x steht für die Zeit, oft auch als t geschrieben.
Was ist das Besondere?
- Der Graph ist eine Sigmoid-Kurve.
- Er hat eine untere und eine obere Schwelle.
- Dazwischen verläuft der Graph schwanenhalsförmig.
- Das modelliert viele Wachstumsprozesse gut.
Warum gehen nicht einfachere Funktionen?
- Einfacher wären zum Beispiel f(x)=ax+b oder f(x)=ab^x.
- Solche Funktionen gehen mit wachsendem x aber gegen unendlich.
- Das würde heißen: ein Bestand wird unendlich groß.
- So etwas gibt es in der Realität eher nicht.
- Das meiste hat eine klare Obergrenze.
- Dazu gibt es die logistische Funktion.
- Ein Beispiel ist eine Epidemie ↗
Wozu gehört die Funktion?
- Zu den Sigmoidfunktionen ↗
Was sind typische Anwendungen?
Offensichtlich ist die modellhafte Mathematisierung begrenzter Wachstumsprozesse als logistische Funktion, etwa die Anzahl infizierter Personen bei einer Pandemie. Eine weitere Anwendung ist die Programmierung eines Schwellenwertes innerhalb von Neuronen in einem neuronalen Netzwerk. Lies mehr unter neuronales Netzwerk ↗
Wie kann man die Formel herleiten?
Die logistische Funktion entsteht aus einer recht einfachen Differentialgleichung. Der Grundgedanke ist, dass sich die Geburtenrate linear, die Todesrate aber quadratisch mit dem Bestand verändert. Dadurch überwiegt bei geringer Populationsgröße das Wachstum, bei großer Populationsgröße stagniert das Wachstum dann aber. Die Herleitung ist sowohl mathematisch als auch historisch ausführlich erläutert in: Harro Heuser: Gewöhnliche Differentialgleichungen. 6. Auflage, 2009. ISBN: 978-3-8348-0705-2. Verlag Vieweg & Teubner. Seite 22ff. Der Heuser ↗
