 Differenzierbar
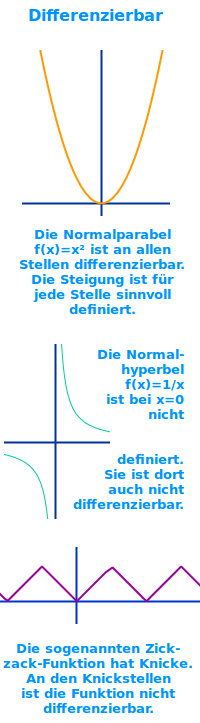
Differenzierbar
Eine Funktion kann abgeleitet werden
Differenzieren ist in der Analysis ein anderes Wort für ableiten, also f'(x) bilden. An Stellen, wo dies für eine Funktion möglich ist, ist die Funktion differenzierbar. Kann man keine erste Ableitung bilden, ist die Funktion dort nicht differenzierbar. Das ist ist hier näher erklärt. => Ganzen Artikel lesen …
… Stelle ohne eindeutige Steigung => Nicht differenzierbar
dy/dx als f'(x)
Die erste Ableitung einer Funktion zu bilden nennt man auch differenzieren. Umgangsprachlich und in den Wirtschaftswissenschaften heißt differenzieren so viel wie die Vielfalt erhöhen oder mehrere Aspekte eines Themas erörtern. Hier wird ausschließlich die Bedeutung des Wortes Differenzieren in der Mathematik besprochen. => Ganzen Artikel lesen …
Übersicht
Differenzierung ist allgemein eine Auffächerung in unterschiedliche Arten, Aspekte oder Gesichtspunkte. Das Bilden der ersten Ableitung in der Mathematik hingegen nennt man differenzieren. Hier stehen verschiedene Bedeutungen aus der Didaktik, Biologie und Mathematik. => Ganzen Artikel lesen …
Analysis
Differenzierbarkeit heißt so viel wie Ableitbarkeit: eine Funktion f(x) kann differenzierbar sein oder auch nicht. Differenzierbar heißt, dass man für alle Punkte des Graphen eine sinnvolle Steigung definieren kann. Rechnerisch heißt das: die h-Methode geht für alle x-Werte auf. Graphisch heißt es, dass man an alle Punkte des Graphen sinnvoll eine Tangente anlgegen kann. Eine ausführliche Erklärung steht unter => differenzierbar
 Nicht differenzierbar
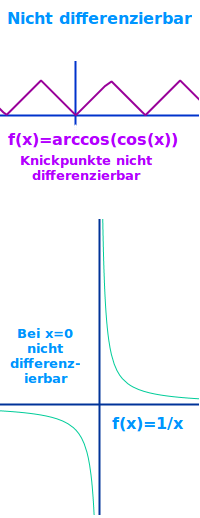
Nicht differenzierbar
Meint: man kann keine Ableitung bilden.
Differenzieren heißt ableiten, also f'(x) bilden. Nicht jede mathematische Funktion ist an allen Stellen differenzierbar: an Ecken, Lücken und Sprüngen kann man zum Beispiel keine Ableitung bilden. Anschaulich heißt das: an einem Punkt lässt sich nicht eindeutig eine Tangente anlegen. => Ganzen Artikel lesen …
… man kann die erste Ableitung bilden, mehr unter => differenzierbar
Mathematik
Das Begriffspaar stetig und differenzierbar gehört zu Funktionen, insbesondere wenn man auch ihre Graphen betrachtet. Eine Funktion ist überall dort stetig, wo sie keine Lücken oder Sprünge im Graphen hat. Sie ist zusätzlich noch differenzierbar, wenn sie dort keinen Knick im Graphen hat. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …

