Skalares Produkt
3 mal den Vektor (4 | 5 | -2) gibt den Vektor (12 | 15 | -6): man multipliziert jede Koordinate des gegebenen Vektors mit der Zahl. Diese Rechnung nennt man das skalare Produkt. Das skalare Produkt ist aber nicht dasselbe wie das sehr ähnlich benannte Skalarprodukt. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
 Zahl
Zahl
Mathematik
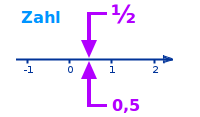
Eine Zahl ist ein Begriff, das heißt eine Vorstellung, von einem Wie-Viel oder Wie-Vielen. Die Zahl selbst ist etwas anderes als ihre Darstellung. Jeder eigene Punkt auf der Zahlengerden ist eine eigene Zahl. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
 Mal
Mal
Anleitung
4+4+4+4+4 ist kurz: 5 mal 4: das Malrechnen, auch multiplizieren oder vervielfachen genannt, ist eine Kurzform für das Plusrechnen mit gleichen Zahlen. => Ganzen Artikel lesen …
 Vektor
Vektor
↗ Definition
Als Vektor bezeichnet man in der Mathematik oft einen Pfeil in einem 2D- oder 3D-Koordinatensystem. Er wird oft mit zwei, drei oder auch mehr Zahlen - den Vektorkoordinaten - geschrieben. Diese Zahlen sagen nichts darüber aus, wo ein Vektor in einem Koordinatensystem liegt. Die Zahlen sagen nur, wie lang der Vektor ist und in welche Richtung er zeigt. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… z. B. 15 als 3·5 schreiben, siehe auch => Zahl faktorisieren
Nicht defniert
12 minus den Vektor (2|4|6) ist nicht defniert, kann also nicht gerechnet werden. Eine reine Zahl im Unterschied zu einem Vektor nennt man auch ein Skalar. Die Subtraktion von Skalaren mit Vektoren ist also nicht definiert. Definiert ist aber => Vektor minus Vektor
Nicht defniert
12 plus den Vektor (2|4|6) ist nicht defniert, kann also nicht gerechnet werden. Eine reine Zahl im Unterschied zu einem Vektor nennt man auch ein Skalar. Die Addition von Skalaren mit Vektoren ist also nicht definiert. Definiert ist aber => Vektor plus Vektor
Malkette
In der Malkette x·14·y·(z+1)·3·v sind die 14 und die 3 Zahlenfaktoren: sie sind Teiler einer Malkette, also Faktoren und zusätzlich reine Zahlen. Dazu steht hier noch ein Beispiel. => Ganzen Artikel lesen …

