==== Definition ====
==== Besonderheit der komplexen Wurzel ==== => Ganzen Artikel lesen …
Wurzel
Definition
Die Wurzel von der Zahl 16 ist die 4. Denn: 4 mal 4 gibt wieder 16. Man schreibt kurz: √16=4. Die Wurzel von irgendeiner Zahl z ist diejenige nicht negative Zahl, die mit sich selbst malgenommen wieder die Zahl ergibt. Diese Definition gilt für die umgangssprachlich gesprochen „normale“ Wurzel, die man auch Quadratwurzel nennt. => Ganzen Artikel lesen …
Ganze Zahlen
Einer sind die Zahlen aus der Einerreihe: 0; 1; 2; 3; 4 und so weiter. Nicht zu den Einern zählen echte Kommazahlen wie 3,4 sowie auch Brüche deren Wert nicht ganzzahlig ist, etwa 3/4 oder 5/9. Einer dürfen aber negativ sein, wie etwa -17 oder -16. => Ganzen Artikel lesen …
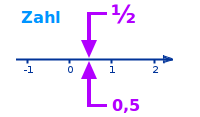
Zahl
Mathematik
Eine Zahl ist ein Begriff, das heißt eine Vorstellung, von einem Wie-Viel oder Wie-Vielen. Die Zahl selbst ist etwas anderes als ihre Darstellung. Jeder eigene Punkt auf der Zahlengerden ist eine eigene Zahl. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… meint dasselbe wie der => Betrag einer komplexen Zahl
… Winkel mit reeller Achse, gleichbedeutend mit dem => Argument einer komplexen Zahl
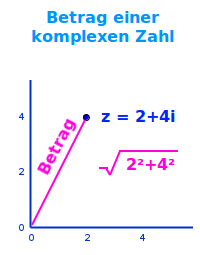
Betrag einer komplexen Zahl
Bedeutung | Schreibweise | Berechnung
Der Betrag |z| einer komplexen Zahl z ist gleich ihrem Abstand vom Koordinatenursprung in der Gaußschen Zahlenebene. => Ganzen Artikel lesen …
… ist nicht definiert, mehr unter => größer und kleiner bei komplexen Zahlen
… z. B. (4+2i)² => komplexe Zahl quadrieren
