 Winkel zwischen Vektoren
Winkel zwischen Vektoren
Definition
Zwei Vektoren a und b sind gegeben. Gesucht ist der Winkel, den sie an einem ihrer gedachten Schnittpunkte haben. Zur Berechnung verwendet man das Skalarprodukt der zwei ektoren, ihre Beträge und den sogenannten Arcuscosinus. Das ist hier erklärt. => Ganzen Artikel lesen …
 Winkel
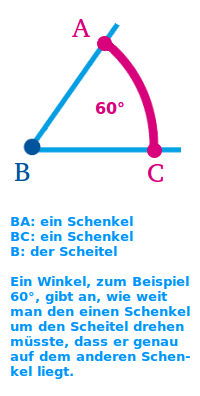
Winkel
Geometrie
Das Zeichen ∠ steht für einen Winkel von vielleicht 50°. Der Winkel als Zahl angegeben sagt, wie groß der Richtungsunterschied zwischen zwei Linien ist [6]. Man kann das auch als Größe einer Öffnung (wie bei Uhrzeigern) deuten [5] oder als Weite einer Drehung [4]. Alle drei Deutungen sind hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …
 Zwischen
Zwischen
Von zwei Seiten begrenzt
In dem Wort PAP steht das große A zwischen den zwei großen P. Hier stehen einige Beispiel sowie mathematische Schreibweisen für zwischen. => Ganzen Artikel lesen …
⊗☉↗⮅ Arten und Einteilung
Vektoren sind gedachte Pfeile in einem 2D-, 3D- oder höherem Koordinatensystem. Sie werden oft aus zwei oder drei Zahlen zusammengesetzt, etwa (4|3|5). => Ganzen Artikel lesen …
Vektorrechnung
Als Winkel zwischen zwei Ebenen ist der kleinstmögliche Winkel definiert, den man mit einem Schnittpunkt der Ebenen als Scheitel und davon ausgehend zwei Linien in je einer der Ebenen als Schenkel bestimmen kann. Dieser Winkel ist immer auch der Winkel zwischen den zwei Normalenvektoren der Ebenen. Ein häufiges Formelzeichen ist das kleine griechische phi (φ). Hier werden verschiedene Lösungswege kurz vorgestellt. => Ganzen Artikel lesen …
2D und 3D
Winkel, auch Schnittwinkel genannt, werden für Geraden in einem xy-Koordinatensystem (2D) oder in einem xyz-Koordinatensystem (3D) berechnet. Beide Fälle werden hier kurz vorgestellt. => Ganzen Artikel lesen …
… Definition und Berechnung unter => Winkel zwischen Vektoren
… Berechnung unter => Winkel über Skalarprodukt
… mit dem Skalarprodukt => Winkel über Skalarprodukt
… siehe unter => Winkel zwischen Vektoren berechnen
Vektorrechnung
Angenommen, ein Vektor wird in seiner Lage zu einer gegebenen Ebene betrachtet. Beide Objekte sind üblicherweise in einem 3D-Koordinatensystem dargestellt. Man kann dann einen Schnittwinkel definieren und über gegebenen Gleichungen diesen Winkel auch berechnen. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …

