 Wellenfunktion
Wellenfunktion
Physik
In der Quantenmechanik ordnet die Wellenfunktion ψ(r,t) Punkten im Raum eine Wahrscheinlichkeit zu, dort - in ihrer Nähe - ein Teilchen anzutreffen. Das wird hier kurz erläutert. => Ganzen Artikel lesen …
 Fehlerfunktion
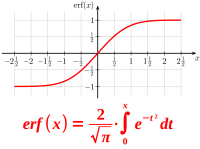
Fehlerfunktion
Wertetabelle
Die Fehlerfunktion oder auch Gaußsche Fehlerfunktion, oft geschrieben als erf(x) ist eine spezielle Sigmoidfunktion. Sie findet vor allem Anwendung in der Statistik. Ausgesprochen ist ihre Gleichung: f(x) = Integral von 0 bis x von 2 durch Wurzel aus pi mal dem Integral von e hoch minus-r-quadrat mal dr. Hier steht eine Wertetabelle. => Ganzen Artikel lesen …
… z. B. „an der Stelle Siehe unter => Stellen von Graphen
Physik
Der Begriff der Weltfunktion wurde spätestens 1912 von dem Physiker Gustav Mie gebraucht. Sie bezeichnet eine Mathematik, die die Maxwellschen Gleichungen der Elektrodynamik mit den Folgerungern von Einsteins Relativitätstheorie und der Materie verbindet und war über zwei Jahrzehnte eine Art Forschungsprogramm für andere Physiker und Mathematiker wie Max Born, David Hilbert [2] oder Ernst Reichenbächer [3]. Ein dabei wichtiger Gedanke ist die Idee der => Wirkung (Physik)
… x < 0 gibt 0, alles andere gibt 1, siehe auch => Heaviside-Funktion
Physik
Als Kollaps der Wellenfunktion [1] oder Zustandsreduktion beschreibt man den Übergang eines quantenmechanischen Systems von einer reinen Wahrscheinlichkeitsverteilung vieler möglicher Zustände hin zu einem tatsächlich gemessenen oder realisierten Zustand. [4] Welcher der möglichen Zustände angenommen wird scheint dem echten Zufall zu unterliegen. [5] Hier wird eine philosophisch interessante Interpretation vorgestellt. => Ganzen Artikel lesen …

