 Umfang
Umfang
Eine Rand- beziehungsweise Umfangslinie
Definition: Man hat eine ebene (flache Figur), die durch eine durchgehende Linie begrenzt ist. Diese Linie nennt man die Rand- oder Umfangslinie. Ihr Länge wird kurz als Umfang bezeichnet. Die übliche Abkürzung ist ein großes U. => Ganzen Artikel lesen …
Beispiele
Erde, Ond, Sonne, Mars: hier stehen einige Beispielwerte: => Ganzen Artikel lesen …
… das große U ist die übliche Abkürzung für einen => Umfang
… ist (2021) die Hauptstadt des Landes => Jordanien
Definition
Die äußere Randlinie eines Rades nennt man den Radumfang. Bei Fährradern wird dieser oft in Zoll angeben (klein: 20 Zoll, groß: 28 Zoll). Der Raddurchmesser mal 3,14 (pi) gibt recht genau den Radumfang. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Himmelskörper
Etwa 40075 Kilometer: die Erde ähnelt von der Form her einer ganz leicht abgeplatteten Kugel. Am Äquator entlang ist ihr Umfang etwas größer als der Umfang durch die Pole. Der Grund ist die Drehung der Erde um sich selbst, die sogenannte Erdrotation. Lies mehr unter => Erdumfang
… Bei Kreisringen: der Umfang des äußeren Kreises, siehe auch => Kreisring
 Bahnumfang
Bahnumfang
Astronomie
Planeten oder andere Körper bewegen sich oft auf Kreis- oder Ellipsenbahnen um einen anderen Körper, den sogenannten Zentralkörper. Der Bahnumfang ist dann die Linie die einmal ganz um den Zentralkörper herumführt. Damit ist der Bahnumfang ein Sonderfall einer Umfangslinie. Siehe als Beispiel die => Mondbahn
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
 Brustumfang von Soldaten
Brustumfang von Soldaten
Historisch
Historische Daten, die zur Entdeckung des Zusammenhanges einer statistischen Normalverteilung mit Messdaten aus der Wirklichkeit führten. => Ganzen Artikel lesen …
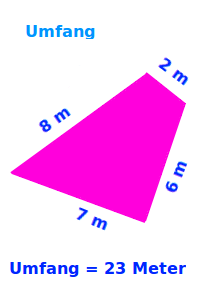
Einmal alle Seiten des Dreiecks abgelaufen
Die Länge aller drei Seiten aufaddiert: der Umfang ist die Länge der Randlinien. => Ganzen Artikel lesen …
… Die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
a+b+c
Zur Berechnung addiert man die Längen der drei einzelnen Seiten. Das Ergebnis ist der => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
a+b+c
Man addiert die Längen aller drei Seiten zusammen. Das Ergebnis ist der => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… siehe unter => Dreiecksumfang
… d = U:Siehe unter => Kreisdurchmesser aus Kreisumfang
… d = U:Siehe unter => Kreisdurchmesser aus Kreisumfang
… d = U:Siehe unter => Kreisdurchmesser aus Kreisumfang
… U = pi mal d, mehr unter => Kreisumfang aus Kreisdurchmesser
… d = U:Siehe unter => Kreisdurchmesser aus Kreisumfang
… d = U:Siehe unter => Kreisdurchmesser aus Kreisumfang
Näherung
Eine Ellipse ist eine Art gestreckter oder gestauchter Kreis. Zur Berechnung der Umfangslänge gibt es keine geschlossene Formeln, es gibt nur Näherungslösungen. Eine ist hier kurz vorgestellt. => Ganzen Artikel lesen …
 Erdumfang
Erdumfang
Etwa 40000 km
40000 km, ausgesprochen als 40 Tausend Kilometer ist in etwa der Erdumfang. Da die Erde aber keine perfekte Kugel ist, gibt es auch verschieden große Erdumfänge. Die Unterschiede sind aber immer sehr klein. Die Angabe ungefähr 40 Tausend Kilometer ist meistens genau genug. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… siehe unter => Eratosthenes
- [1] Eratosthenes and the Circumference of the Earth. Nature 152, 473 (1943). https://doi.org/10.1038/152473a
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… Durchmesser mal Pi gibt Umfang, mehr unter => Kreisumfangsformel
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang

