Definition
Augend + Addend = Summe oder auch: Summand + Summand = Summe: bei 4+1 = 5 ist sowohl die Plusaufgabe 4+1 wie auch ihr Ergebnis 5 eine Summe. Möchte man zwischen den beiden Unterscheiden, spricht man von Summenterm (4+1) und seinem Summenwert (5). Das ist hier näher erklärt. => Ganzen Artikel lesen …
Kurzinfo | Beispiele
Summen sind Plusaufgaben oder deren Ergebnisse. Den Ausdruck 3+4+1 kann man eine Summe nennen. Aber auch sein Ergebnis 8 heißt Summe (oder Summenwert). => Ganzen Artikel lesen …
Physik
Als Dummy bezeichnet man eine Attrappe, ein Modell, meist von einem Menschen. Das Ziel ist es oft, die Wirkung physikalischer Vorgänge auf einen menschlichen Körper zu untersuchen. Siehe auch => WH54 20250719 Inventar Dummies
… eine Gemme ist eine => Edelstein
… anderes Wort für das Schüttgutmaß => Scheffel
Sumer
Landschaft
Als Sumer bezeichnet man die geographische Region am Unterlauf der Flüsse Euphrat und Tigris, in etwa zwischen der heutigen Stadt Bagdad und dem Persischen Golf. In dieser Region entstand die weltweit erste Hochkultur mit großen Städten und zentralisierten Herrschaftsformen. Lies mehr unter => Sumerer
Anleitung
f(x) = x² + 4x gibt abgeleitet f'(x) = 2x+4: die allgemeine Regel ist, dass man die Teile einer Plus- oder Minuskette, im Prinzip also die Summanden, für sich einzeln ableiten kann. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… so etwas wie 1+2+3+4+5+6 .Siehe unter => Summenformeln
… gibt es für die Siehe unter => teilbar durch elf
Anleitung
f(x) = 4x + 3 wird aufgeleitet zu F(x) = 4·½·x²+3·x: die Glieder [1] einer Pluskette, einer Minuskette oder einer gemischten Plusminuskette kann man einzeln für sich aufleiten. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Augensumme
Würfel
Alle Punkte mehrerer Würfel zusammengerechnet nennt man die Augensumme. Dabei zählt man aber nur die Augen, die oben liegen. Ein Würfel mit einer 4 und ein Würfel mit einer 1 haben gemeinsam die Augensumme 5. Interessant ist noch folgende Besonderheit. Beinem normalen Spielwürfel ist die Summe der Augen von zwei einander gegenüberliegenden Seiten immer 7. Das heißt: gegenüber von der 5 ist die 2. Und gegenüber von der 6 liegt immer die 1. Siehe auch => Spielwürfel
… Summe aller Ausgänge =Siehe unter => Summenregel für Ausgänge
… Summe aller Ausgänge =Siehe unter => Summenregel für Ausgänge
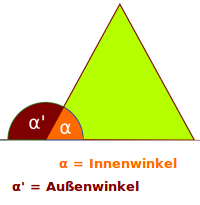Außenwinkelsumme
Geometrie
Von jeder Ecke ein Außenwinkel und diese zusammengerechnet ergibt die Außenwinkelsumme. Das ist hier kurz für Dreiecke sowie auch für allgemeine Vielecke erklärt. => Ganzen Artikel lesen …
Ergibt immer 900 Grad
Jedes Dreieck hat immer drei Außenwinkel: an jeder Ecke einen. Die Außenwinkel liegen immer außerhalb des Dreiecks. => Ganzen Artikel lesen …
… Bei 3+4 heißen 3 und 4 => Summanden
… Bei 3+4 heißen 3 und 4 => Summanden
Definition
Im Zusammenhang mit Unternehmen ist die Bilanzsumme die Summe der Vermögensgegenstände auf der Aktivseite bzw. die Summe des Gesamtkapitals auf der Passivseite einer Bilanz zum Bilanzstichtag. Beide Summen sind imme gleich groß. Siehe auch => Bilanz
… man 3/4+5/8 rechnet steht unter => Brüche addieren
Cerro Negro Aschensumme
Datenliste
Proportionalität: der Cerro Negro ist ein eher kleiner aber recht aktiver Vulkan in Nicaragua. Geologen haben rund um den Vulkan untersucht, wie dick die Asche auf dem Boden abgelagert war. Je weiter weg vom Vulkan sie waren, desto dünner war die Aschelage. Für die Aschelagen der älteren Ausbrüche mussten sie dabei natürlich im Boden etwas nach unten graben. Unten stehen ihre Ergebnisse. => Ganzen Artikel lesen …
Tabellen
Alles was schräg in einer Reihe steht aufaddiert: das Wort Diagonalensumme wird im Zusammenhang mit Tabellen werden. In einer Tabelle werden Zahlen in einem Gittermuster angeordnet. Dabei entstehen Diagonalen: das sind alle Zahlen, die von links oben nach rechts unten oder von links unten nach rechts oben gesehen in einer Reihe stehen, zum Beispiel in einem magischen Quadrat (hier kurz erklärt). => Ganzen Artikel lesen …
… etwas zusammenrechnen und das Ergebnis hinschreiben, also eigentlich wie => addieren
… Definition und Unterschied unter => Differenzterm oder Differenzwert
Doppelsumme
ΣΣ
Eine Doppelsumme, angezeigt durch ein doppelt geschriebenes großes griechisches Sigma Σ genannt, ist eine mathematische Notation, bei der das Summenzeichen zweimal hintereinander verwendet wird, um die Summe aller Elemente einer zweidimensionalen Struktur, wie einer Matrix oder Tabelle, zu berechnen. Es wird häufig verwendet, um beispielsweise alle Elemente einer Matrix aufzusummieren, wobei die Summation zeilen- oder spaltenweise erfolgt. Die äußere Summe wird dabei nach dem ersten Index (z. B. i) durchlaufen, während die innere Summe nach dem zweiten Index (z. B. j) iteriert. => Ganzen Artikel lesen …
… siehe unter => Winkelsumme in Dreieck
… => Winkelsumme
… gibt immer 180 Grad, mehr unter => Innenwinkelsumme für Dreiecke
… Summe aller Ausgänge =Siehe unter => Summenregel für Ausgänge
… z. B. 9 = 4+3+2
Faktorisieren heißt: in eine Malkette zerlegen: 20 faktorisiert ist z. B. 4·5 oder 2·10. Man kann jede Zahl und jeden Term auch als Pluskette schreiben: 20x kann man zum Beispiel als 18x+2x schreiben. Die Pluskette als Ganzes ist dann eine Summe oder ein Summenterm. Die einzelne Teile heißen Summanden oder auch Glieder. Mehr unter => zerlegen
Physik
Dass die Summe der Innenwinkel in einem Dreieck immer exakt 180° gilt nicht immer. Bereits der Mathematiker Gauß zweifelte die Gültigkeit an. Gründe für diesen Zweifel und Konsequenzen für unser Weltbild sind hier erklärt. => Ganzen Artikel lesen …
… zum Berechnen, siehe unter => Innenwinkelsummenformeln
… Für z. B. 1+2+3+4+5+6, siehe unter => Summenformeln
… so etwas wie 1+2+3+4+5+6 .Siehe unter => Summenformeln
… zum Berechnen, siehe unter => Innenwinkelsummenformeln
… so etwas wie 1+2+3+4+5+6 .Siehe unter => Summenformeln
