Steigung in einem Punkt
Interpretation
Kurzdefinition: Funktionsgraphen können an unterschiedlichen Punkten unterschiedlich steil sein. Wie steil ein Graph an genau einem Punkt ist nennt man auch den Ableitungswert, oft kurz auch nur die Ableitung oder eindeutiger: die Steigung in einem Punkt. Diese Steigung kann beliebige - auch negative - Zahlenwerte annehmen. => Ganzen Artikel lesen …
Steigung
Übersicht
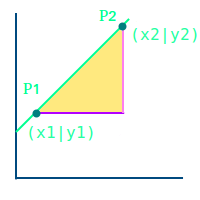
Steigung sagt, wie steil etwas nach oben oder unten geht. Man kann eine Steigung als Zahl angeben, zum Beispiel: etwas hat eine Steigung von 2,5. Das meint: Eine Strecke geht zweieinhalb mal so weit senkrecht nach oben wie waagrecht nach vorne. Es werden verschiedene Gebiete aus der Mathematik vorgestellt. => Ganzen Artikel lesen …
Übersicht
In als das Element Indium oder die Umwandlung einer Zahl oder Einheit in eine andere Art: das Wort in hat verschiedene Bedeutungen. Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Mathematik
Dezimalpunkt, Tausendertrennpunkt und Multiplikations-Punkt: diese drei wichtigen Bedeutungen sind hier kurz erklärt. Viele weitere Bedeutungen stehen unter => Punkte
… z. B. f'(4), siehe unter => Steigung in einem Punkt
… steht unter => Steigung in einem Punkt
Vektorrechnung
Eine Figur, ein Objekt im Sinne der Geometrie, wird an einem Punkt, dem Symmetriepunkt, gespiegelt: von jedem Punkt einer gegebenen Figur geht man in einer geraden Linie bis zum Symmetriepunkt. Von dort aus geht man in derselben Richtung dieselbe Strecke noch einmal. Das Ende dieses Weges markiert dann den gespiegelten Punkt. Diese Art der Spiegelung bezeichnent man meist als => Punktspiegelung
… steht unter => Steigung in einem Punkt
Analysis
Die Steigung in einem Punkt meint die Steigung eines Graphen einer Funktion an genau einem Punkt. Dazu sind hier kurz einige Verfahren aufgelistet. => Ganzen Artikel lesen …
