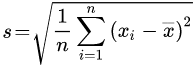Standardabweichung berechnen
Übersicht
Die Standardabweichung Sigma kann für Datenreihen (Zahlenlisten) aber auch aus anderen gegebenen Werten berechnet berechnet werden. Hier werden kurz verschiedene Formeln dazu vorgestellt. => Ganzen Artikel lesen …
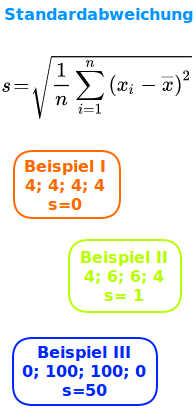Standardabweichung
σ: Ein Streuungsmaß aus der Statistik
Die Standardabweichung Sigma gibt an, wie weit die Zahlen einer Zahlenliste von ihrem gemeinsamen Mittelwert entfernt sind. Die Zahlenliste 3;3;3;3 hat eine Standardabweichung von 0. Die Zahlenliste 1;1;5;5 hat eine Standardabweichung von 2. Hier wird kurz erklärt, was die Standardabweichung als Streuungsmaß bedeut und wie man sie berechnet. => Ganzen Artikel lesen …
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
… mehrere Möglichkeiten unter => Standardabweichung berechnen
Zahlenbeispiele
Hier stehen einige Zahlenlisten mit dazu ausgerechneter Standardabweichung. Damit lassen sich Formeln überprüfen und ein Gefühl für die Bedeutung entwickeln. => Ganzen Artikel lesen …
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… Erklärung mit Zahlenbeispiel unter => Varianz aus Standardabweichung
