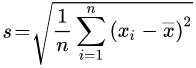Standardabweichung aus Datenliste
Berechnung
Zum Beispiel für die Liste der Zahlen 4, 7 und 10: wie man das das kleine Sigma oder s berechnet, wenn man eine Datenliste, das heißt eine Liste aus Zahlen, gegeben hat: das ist hier kurz mit einem Zahlenbeispiel erklärt. => Ganzen Artikel lesen …
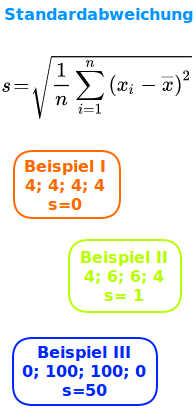Standardabweichung
σ: Ein Streuungsmaß aus der Statistik
Die Standardabweichung Sigma gibt an, wie weit die Zahlen einer Zahlenliste von ihrem gemeinsamen Mittelwert entfernt sind. Die Zahlenliste 3;3;3;3 hat eine Standardabweichung von 0. Die Zahlenliste 1;1;5;5 hat eine Standardabweichung von 2. Hier wird kurz erklärt, was die Standardabweichung als Streuungsmaß bedeut und wie man sie berechnet. => Ganzen Artikel lesen …
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Datenliste
Berechnung
Die Varianz und daraus die Wurzel gibt die Standardabweichung. Wenn die Varianz 4,0 ist, dann ist die Standardabweichung 2,0. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… ist in der Statistik die => Varianz
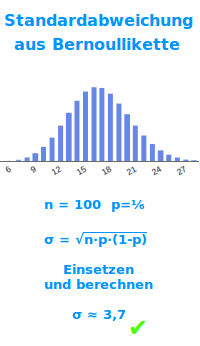Standardabweichung aus Bernoulli-Kette
σ = √(n·p·(1-p))
Einer Binomialverteilung liegt immer einer Bernoulli-Kette als Modell zugrunde. Die Formel oben gilt deshalb sowohl für Bernoulli-Ketten als auch Binomialverteilungen. Eine ausführliche Erklärung steht unter => Standardabweichung aus Binomialverteilung
Zahlenbeispiele
Hier stehen einige Zahlenlisten mit dazu ausgerechneter Standardabweichung. Damit lassen sich Formeln überprüfen und ein Gefühl für die Bedeutung entwickeln. => Ganzen Artikel lesen …
