Spatvolumen berechnen
Grundfläche mal Höhe | Spatprodukt
Ein Spat ist ein sechsflächiger Körper. Die 6 Seitenflächen sind viereckig. Gegenüberliegende Flächen sind immer parallel zueinander. Das Fremdwort für Spat ist Parallelepiped. => Ganzen Artikel lesen …
Das Volumen eines Parallelepipeds
Ein Spat ist ein sechsflächiger Körper bei dem die gegenüberliegende Seiten immer parallel zueinander sind (Art 3D-Parallelogramm). Das Volumen kann man berechnen über Grundfläche mal Höhe oder Alternativ über die Vektorrechnung (Spatprodukt). Mehr unter => Spatvolumen berechnen
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
Volumen berechnen
Übersicht zu Methoden
Ein Volumen gibt an, wie viel Rauminhalt ein Körper hat, wie „groß“ ein Loch oder Hohlraum ist oder wie viel Flüssigkeit beziehungsweise Gas man meint. Es werden einige Methoden zur Berechnung kurz vorgestellt. Die anschauliche Bedeutung ist erklärt unter => Volumen
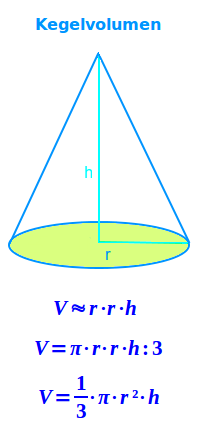
Kegelvolumen berechnen
V = ⅓ · π · r² · h
V = ⅓·π·r²·h ist die Formel für das Volumen eines Kegels. Ein Kegel ist ein spitzer Körper (pyramidenartig) aber mit einem Kreis als Grundfläche. Die Formel ist hier näher erklärt. => Ganzen Artikel lesen …
Kistenvolumen berechnen
V = Länge mal Breite mal Höhe
Eine rechteckige Kiste (quaderförmig) hat eine Länge l, eine Breite b und eine Höhe h. Die Rechnung l mal b mal h gibt das Volumen der Kiste. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… siehe unter => Torusvolumen
