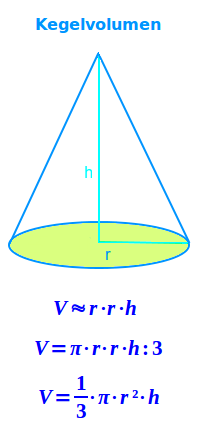
Kegelvolumen berechnen
V = ⅓ · π · r² · h
Basiswissen
V = ⅓·π·r²·h ist die Formel für das Volumen eines Kegels. Ein Kegel ist ein spitzer Körper (pyramidenartig) aber mit einem Kreis als Grundfläche. Die Formel ist hier näher erklärt.
Formeln
◦ V = r · r · h (etwa)
◦ V = π · r · r · h : 3 (genau)
◦ V = ⅓ · π · r² · h (genau)
Legende
◦ V = Zum Beispiel in cm³ ist das => Kegelvolumen
◦ π = Sprich "pi", etwa 3,14, die => Kreiszahl
◦ r = Zum Beispiel in cm, von der Grundfläche der => Kreisradius
◦ h = Senkrecht von der Spitze zum Boden => Kegelhöhe
Einheiten
◦ 1 Liter ist wie 1000 cm³
◦ 1 Liter ist wie 1000 ml
◦ 1 ml ist wie 1 cm³
◦ 1 dm³ ist wie 1000 cm³
◦ 1 dm³ ist wie 1000 ml
◦ 1 dm³ ist wie 1 Liter
◦ 1 m³ ist wie 1000 Liter
Rechenbeispiel Vulkankegel
Der Vulkan Semeru liegt auf der Insel Java, nahe am Äquator. Der Vulkan hat in etwa die Formel eines Kegel. Nur ein kleiner Teil der Spitze fehlt, nämlich an der Stelle des Vulkankraters. Der Semeru zählt zu den aktivsten und gefährlichsten Vulkanen der Welt. Er erhebt sich Kegelförmig über sein vergleichsweise flaches Umland. Die grob kreisförmige Grundfläche hat einen Durchmesser von etwa 3,6 km, der Radius ist also 1,8 km [1]. Die Höhe der Kegelform liegt dann bei rund 1000 Meter. Das ergibt ein Kegelvolumen von rund 3,4 Kubikkilometer, kurz 3,4 km³. Zum Vergleich siehe auch => Kubikkilometer
Wie ist Kegelvolumen definiert?
Das Volumen kann einmal die Flüssigkeit bedeuten, die man von innen in einen Kegel hineinlaufen lassen könnte. Man spricht dann vom Volumen als Hohl- oder Flüssigkeitsmaß. Das Kegelvolumen kann aber auch angeben, wie wie Raum der Kegel als Ganzes einnimmt. Anschaulich wäre das, wie viel Wasser er untergetaucht verdrängen würde. Lies mehr zur Definition unter => Kegelvolumen
Quellen
◦ [1] Der Durchmesser wurde über eine Messung auf Google Maps bestimmt. Der Rand der Kegelform wurde graphisch der Darstellung mit Höhenlinien entnommen. Die Höhenlinie bei 2700 m ist mehr oder minder kreisförmig.
