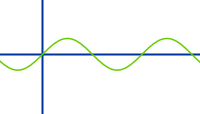
Sinusfunktion
=> Ganzen Artikel lesen …
Cosinusfunktion
f(x) = cos(x)
f(x) = cos(x) nennt man auch die einfache oder elementare Cosinusfunktion. Hier stehen einige ihrer Eigenschaften kurz aufgelistet. => Ganzen Artikel lesen …
Einsfunktion
f(x)=1
Ordnet jedem x-Wert die Zahl 1 als Funktionswert zu. Der Graph ist eine horizontale Linie parallel zur x-Achse. => Ganzen Artikel lesen …
Kardinalsinus
si(x) steht für den nichtnormierten Sinus cardinalis. sinc(x) ist der normierte sinus cardinalis. => Ganzen Artikel lesen …
Beispiele
Sin, sinc, si oder auch die Keeling-Kurve oder die Wellengleichung: hier stehen einige Arten und Beispiele der trigonometrischen Sinusfunktion als Beispiel. => Ganzen Artikel lesen …
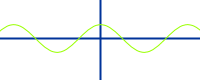
Allgemeine Sinusfunktion
Definition
f(x) = a·sin(bx+c) - ausgehend von der elementaren Sinusfunktion kann eine allgemeine Sinusfunktion definiert werden. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
f'(x) = cos(x)
Die elementare Cosinusfunktion f(x) = cos(x) abgeleitet gibt f'(x) = -sin(x). Enthält das Argument einen komplexeren Term, benutzt man noch die Kettenregeln: f(x) = cos(4x²-8x) gibt abgeleitet f'(x) = -(8x-8)·sin(4x²-8x). Lies mehr dazu unter => Ableiten über Kettenregel
… gibt sin(Siehe unter => cosinus x aufgeleitet
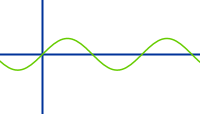Die Sinusfunktion
f(x) = sin(x)
Die Sinusfunktion - mit vorangestellten Artikel - bezeichnet die einfache oder auch elementar genannte Sinusfunktion f(x)=sin(x). Diese Funktion ist hier kurz mit ihren Eigenschaften vorgestellt. => Ganzen Artikel lesen …
… -cos(Siehe unter => sinus x aufgeleitet
… f(x) = cos(x), siehe auch => Cosinusfunktion
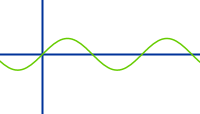Einfache Sinusfunktion
… Name für die Funktion => f(x)=sin(x)
… f(x)=cos(Siehe unter => Cosinusfunktion
… die „einfachste“ aller Sinusfunktion, Graph unter => f(x)=sin(x)
… siehe unter => Allgemeine Sinusfunktion
… Erklärung und Graph unter => f(x)=sin(x)
… Erklärung und Graph unter => f(x)=sin(x)
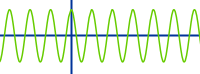
… Definition unter => Periode bei Sinusfunktion
Definition
Der kürzeste Abstand auf der x-Achse nach dem sich ein Muster der Sinuskurve erneut wiederholt. Dieser Periodenabstand bezeichnet man oft mit einem großen lateinischen T. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… Definition unter => Periode bei Sinusfunktion
… Definition unter => Periode bei Sinusfunktion
… Definition unter => Periode bei Sinusfunktion
… Definition unter => Periode bei Sinusfunktion
… Definition unter => Periode bei Sinusfunktion
… Definition unter => Periode bei Sinusfunktion
… Definition unter => Periode bei Sinusfunktion
… Definition unter => Periode bei Sinusfunktion
… Erklärung und Graph unter => f(x)=sin(x)
… ist cos (x), mehr unte => Sinusfunktion ableiten
f'(x) = cos(x)
Die elementare Sinusfunktion f(x) = sin(x) abgeleitet gibt f'(x) = cos(x). Enthält das Argument einen komplexeren Term, benutzt man noch die Kettenregeln: f(x) = sin(4x²-8x) gibt abgeleitet f'(x) = (8x-8)·sin(4x²-8x). Lies mehr dazu unter => Ableiten über Kettenregel
… Erklärung und Graph unter => f(x)=sin(x)
… Erklärung und Graph unter => f(x)=sin(x)
… Definition unter => Periode bei Sinusfunktion
… Definition unter => Periode bei Sinusfunktion
… Definition unter => Periode bei Sinusfunktion
