 Sinus
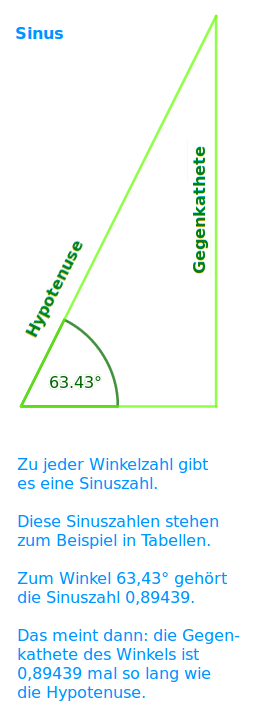
Sinus
Gegenkathete durch Hypotenuse
Der Sinus ist ein Zahl die zu einem Winkel in einem rechwinkligen Dreieck gehört. Sie sagt, wie viel mal so lang die dem Winkel gegenüberliegende Kathete ist wie die Hypotenuse. => Ganzen Artikel lesen …
 Minus
Minus
Abziehen
Drei minus eins gibt zwei: minus heißt, dass man etwas abziehen oder wegnehmen soll. Man soll dann sagen, wie viel danach noch übrig ist. => Ganzen Artikel lesen …
Begriffsklärung
In der Mathematik ist ein Conus ein kegelartiger Körper. In der Biologie bezeichnet das Wort eine bestimmte Art von Sehzellen. => Ganzen Artikel lesen …
 Cosinus
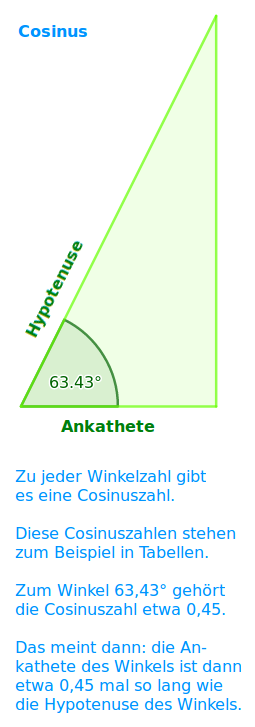
Cosinus
Definition
Ankathete durch Hypotenuse: der Cosinus im engeren Sinn gehört immer zu einem festen Winkel in einem rechtwinkligen Dreieck. Zu jeder möglichen Winkelzahl (0 bis 90) gibt es einen dazugehörigen Cosinuswert. Man liest ihn zum Beispiel aus einer Tabelle ab. Der Wert liegt immer zwischen 0 und 1 und sagt, wie viel mal so lang die Ankathete des Winkels ist, wie die Hypotenuse. => Ganzen Artikel lesen …
… Sinusse ist laut Duden (2022) eine korrekte Mehrzahl des Wortes => Sinus
… Etwa 0.017447, siehe auch => Sinustabelle Grad
… Genau 0, siehe auch => Sinustabelle Grad
ist: -sin(x)
ist: cos(x)
ist: cos(x)
 Allgemeine Sinusfunktion
Allgemeine Sinusfunktion
Definition
f(x) = a·sin(bx+c) - ausgehend von der elementaren Sinusfunktion kann eine allgemeine Sinusfunktion definiert werden. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
 Ankathete über Cosinus
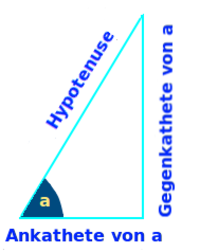
Ankathete über Cosinus
Berechnung
Man hat ein rechtwinkliges Dreieck. Einer der beiden nicht-90°-Grad-Winkel ist bekannt. Die kürzere der zwei Seiten direkt an diesem Winkel ist die sogenannte Ankathete. Sie berührt immer den Winkel. Es wird gezeigt, wie man ihre Länge berechnet. => Ganzen Artikel lesen …
Sinus rückwärts
Der Arcussinus ist die Umkehrung des Sinus. Man fragt nicht nach dem Sinuswert für einen bestimmten Winkel. Man fragt vielmehr: welcher Winkel gehört zu einem bestimmten Sinuswert? Mehr unter => Winkel über Sinus
Definition
Der Areakosinus hyperbolicus, kurz auch arcosh oder acosh ist die Umkehrfunktion des => Kosinus hyperbolicus
Definition
Der Areasinus hyperbolicus, kurz auch arsinh oder asinh ist die Umkehrfunktion des => Sinus hyperbolicus
Winkel
Der Arkuscosinus, auch cos-hoch-minus-eins, gibt an, welcher Winkel zu einem Cosinuswert gehört: man hat den Cosinuswert eines Winkels gegeben. Man will nun wissen, welcher Winkel diesen Cosinus hat. Die Funktion Arkuscosinus gibt genau diesen Winkel zurück. => Ganzen Artikel lesen …
Winkel
Der Arkussinus, auch sin-hoch-minus-eins, gibt an, welcher Winkel zu einem Sinuswert gehört: man hat den Sinuswert eines Winkels gegeben. Man will nun wissen, welcher Winkel diesen Sinus hat. Die Funktion Arkussinus gibt genau diesen Winkel zurück. => Ganzen Artikel lesen …
… gibt sin(Siehe unter => cosinus x aufgeleitet
… -cos(Siehe unter => sinus x aufgeleitet
… gibt sin(Siehe unter => cosinus x aufgeleitet
… gibt sin(Siehe unter => cosinus x aufgeleitet
… -cos(Siehe unter => sinus x aufgeleitet
… -cos(Siehe unter => sinus x aufgeleitet
… gibt sin(Siehe unter => cosinus x aufgeleitet
… -cos(Siehe unter => sinus x aufgeleitet
Skript
Das folgende Bash-Skript simuliert auf dem Bildschirm eine senkrechte und eine waagrechte Sinusbewegung sowie die daraus resultierende Kreisbewegung. => Ganzen Artikel lesen …
Vektorrechnung
Als Cosinus-Ähnlichkeit bezeichnet man einen Zahlenwert zwischen -1 und 1, der für die Ähnlichkeit von zwei Wortfolgen steht. Je ähnlicher sich zwei Wortfolgen, etwa Sätze, sind desto näher liegt der Wert bei 1. Mit Hilfe der Vektorrechnung läßt sich die Ähnlichkeit recht unkompliziert berechnen. Das ist hier mit einem Beispiel vorgestellt. => Ganzen Artikel lesen …
… Genau 1, siehe auch => Cosinustabelle Grad
… Etwa 0.999847, siehe auch => Cosinustabelle Grad
… Genau 0, siehe auch => Cosinustabelle Grad
… Genau 0, siehe auch => Cosinustabelle Grad
… Genau 1, siehe auch => Cosinustabelle Grad
… Etwa 0.707106, siehe auch => Cosinustabelle Grad
… Genau 0, siehe auch => Cosinustabelle Grad
… cos(x) abgeleitet gibt -sin(x). Siehe auch => Ableitungen [Beispiele]

