Scheitelpunkt einer Parabel
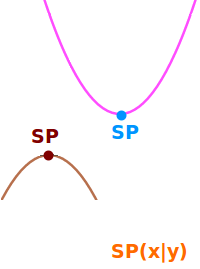
Höchster oder tiefster Punkt
Eine Parabel meint hier den Graphen einer quadratischen Funktion. Der Scheitelpunkt ist dann immer der höchste oder tiefste Punkt dieser Parabel, also entweder der Hoch- oder Tiefpunkt der Parabel. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Scheitelpunkt
Mathematik
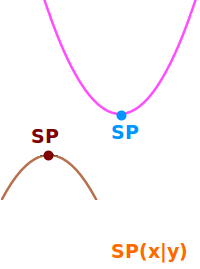
Bei Funktionsgraphen ist ein Scheitelpunkt (SP) der höchste oder tiefste Punkt einer Parabel. Neben dieser Bedeutung gibt es aber auch noch weitere. => Ganzen Artikel lesen …
Ganze Zahlen
Einer sind die Zahlen aus der Einerreihe: 0; 1; 2; 3; 4 und so weiter. Nicht zu den Einern zählen echte Kommazahlen wie 3,4 sowie auch Brüche deren Wert nicht ganzzahlig ist, etwa 3/4 oder 5/9. Einer dürfen aber negativ sein, wie etwa -17 oder -16. => Ganzen Artikel lesen …
Parabel
Analysis
In der Schulmathematik ist die Parabel meist der Graph einer quadratischen Funktion, z. B. von f(x)=x²+2) [1]. Daneben gibt es aber noch weitere Bedeutungen [2], die hier auch kurz vorgestellt werden. => Ganzen Artikel lesen …
… passt am ehesten auf den => Scheitelpunkt einer Parabel
Scheitelpunkte von Parabeln
Beispiele
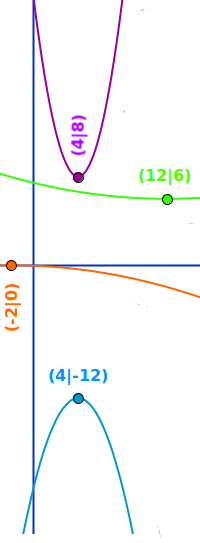
Der höchste und der tiefste Punkt einer Parabel heißt Scheitelpunkt. Man kann ihn aus einem Graphen ablesen, über die quadratische Ergänzung bestimmen oder auch mit Hilfe der ersten Ableitung f'(x). Hier stehen einige Beispiele von quadratischen Funktionen mit ihre Scheitelpunkten. => Ganzen Artikel lesen …
… siehe unter => Scheitelpunktform der Parabelgleichung
… siehe unter => Scheitelpunkt ablesen
… f(x)=Ax²+Bx+C => Scheitelpunkt aus allgemeiner Form
Scheitelpunkt einer Parabel berechnen
… graphisch, rechnerisch, siehe unter => Scheitelpunkt einer Parabel bestimmen
Scheitelpunkt einer Parabel bestimmen
Methoden
Der höchste oder tiefste Punkt einer Parabel ist ihr Scheitelpunkt. Er liegt in der Mitte zwischen den zwei Parabelästen. Einen Scheitelpunkt zu bestimmen heißt, seine x- und seine y-Koordinaten anzugeben, etwa als (2|4). Hier stehen verschiedene Methoden dazu. => Ganzen Artikel lesen …
… f(x)=Ax²+Bx+C => Scheitelpunkt aus allgemeiner Form
