Scheitelpunkt aus Allgemeiner Form
Bestimmen
Gegeben ist eine quadratische Funktion in allgemeiner Form, zum Beispiel f(x) = 4x²-16x+20. Der Graph ist nach oben geöffnet und der Scheitelpunkt liegt bei (2|4). Hier stehen verschiedene Verfahren, wie man diesen Scheitelpunkt bestimmen kann. => Ganzen Artikel lesen …
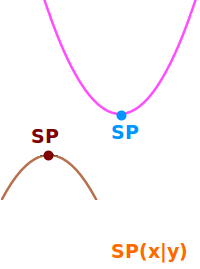
Scheitelpunkt
Mathematik
Bei Funktionsgraphen ist ein Scheitelpunkt (SP) der höchste oder tiefste Punkt einer Parabel. Neben dieser Bedeutung gibt es aber auch noch weitere. => Ganzen Artikel lesen …
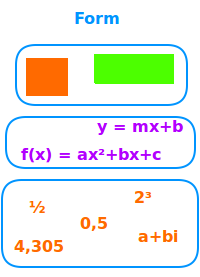Form
Mathematik
Die Gestalt einer Figur, eine Gleichung oder auch Zahlen: in der Mathematik bezieht sich das Wort Form auf verschiedene Dinge. Das ist hier einzeln vorgestellt. => Ganzen Artikel lesen …
… Rechenbeispiel unter => Allgemeine Form in Scheitelpunktform
… f(x)=Ax²+Bx+C => Scheitelpunkt aus allgemeiner Form
… f(x)=Ax²+Bx+C => Scheitelpunkt aus allgemeiner Form
… f(x)=Ax²+Bx+C => Scheitelpunkt aus allgemeiner Form
Verfahren
f(x) = ax²+bx+cx+d ist gegeben, also eine quadratische Funktion in allgemeiner Form, auch Parabelgleichung genannt. Gesucht ist der höchste oder tiefste Punkt, also der Scheitelpunkt. Hier stehen vier Methoden dazu. => Ganzen Artikel lesen …
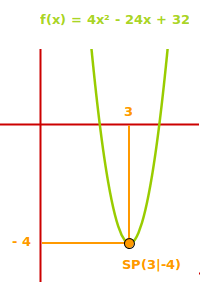
Scheitelpunkt aus Allgemeiner Form über QE
f(x)=4x²-24x+32 umformen in f(x)=4(x-3)²-4
In der Mathematik, Physik oder Chemie: kurze Erklärung von Fachworten, Symbolen und Formeln => Ganzen Artikel lesen …
