 Satz des Pythagoras
Satz des Pythagoras
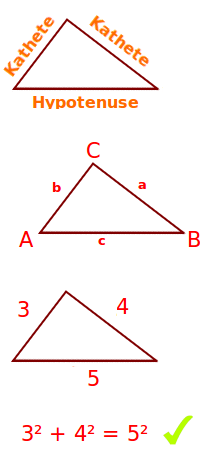
a² + b² = c²
a² + b² = c² ist der Satz des Pythagoras kurz als Formel [3] geschrieben: man hat ein rechtwinkliges Dreieck mit drei Seiten: a, b und c. Das kleine c steht dabei für die längste Seite, die Hypotenuse. Man misst die Länge jeder der drei Seiten. Dann multipliziert man die Länge jeder Seite mit sich selbst, quadriert sie also. Man erhält drei Zwischenergebnisse: a², b² und c². Dann addiert man a² und b². Die daraus entstehende Summe ist immer gleich (oder sehr nahe bei) c². Kurz: a²+b² = c² => Ganzen Artikel lesen …
Mathematisch
In der Grammatik ist ein Satz eine Aussage mit einem Subjekt und einem Verb: „Peter rennt“. Der Satz kann wahr sein (Peter rennt tatsächlich) oder auch falsch (Peter rennt nie, er ist zum Beispiel ein Fisch). Ein Satz ist damit etwas anderes als ein Gesetz, eine Hypothese oder eine Theorie. Ein Lehrsatz in der Mathematik ist eine immer wahre Aussage, die man durch logische Schlüsse bewiesen hat. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Philosoph
Pythagoras war ein antiker griechischer Mathematiker und Philosoph. Sein Name ist verbunden mit dem Satz des Pythagors a²+b²=c². Mehr zur Person unter => Pythagoras von Samos
Länge der Kathete a berechnen
Kennt man von einem rechtwinkligen Dreieck die Länge der Hypotenuse (längste Seite) sowie die Länge einer der beiden anderen Seiten (Katheten), kann man die Länge der dritten Seite (a) ausrechnen. Mehr über => Kathete über Pythagoras
Vektorrechnung
Mit Hilfe einer Art von dreidimensionalem Satz des Pythagoras kann man den Abstand von zwei Punkten im Raum sowie die Länge von Vektoren in einem Raum berechnen. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Länge der Kathete b berechnen
Kennt man von einem rechtwinkligen Dreieck die Länge der Hypotenuse (längste Seite) sowie die Länge einer der beiden anderen Seiten (Katheten), kann man die Länge der dritten Seite (b) ausrechnen. Mehr über => Kathete über Pythagoras
Drei Lehrsätze, auch Flächensätze genannt
Kurz erklärt: gilt für alle - und nur für - rechtwinklinge Dreiecke: der Satz des Pythagoras, der Höhensatz und der Kathetensatz. Hier steht eine kurze Übersicht. => Ganzen Artikel lesen …
… siehe => Kiste 17
Wie man eine unbekannte Katheten-Länge ausrechnet
Wenn man von einem rechtwinkligen Dreieck die Länge der Hypotenuse und die Länge einer der beiden Katheten kennt, dann kann man die Länge der unbekannten Kathete immer so ausrechnen: => Ganzen Artikel lesen …
… Rechenweg auf => Kathete über Pythagoras
Wie man eine unbekannte Hypotenusenlänge ausrechnet
Wenn man von einem rechtwinkligen Dreieck die Länge der beiden Katheten kennt, dann kann man die Länge der Hypotenuse immer so ausrechnen: => Ganzen Artikel lesen …
a³+b³=c³
a³+b³=c³: kann man für a, b und c jeweils eine natürliche Zahl einsetzen - die Zahlen dürfen unterschiedlich sein - und die Gleichung geht am Ende auf? Mit dieser Frage beschäftigten sich Mathematiker über Jahrhunderte. Das ist hier kurz erläutert. => Ganzen Artikel lesen …
Sammlung
Zeichne eine Skizze und versuche rechtwinklige Dreiecke darin zu finden. Benenne die Hypotenuse am besten mit c und die beiden Katheten mit a und b. => Ganzen Artikel lesen …

