Quotient
Definition
Divididen geteilt durch Divisor = Quotient: bei 8:2=4 ist eine Aufgabe mit eine Quotienten. Als Quotient bezeichnet man sowohl jede geteilt-Aufgabe sowie auch das Ergebnis, das dabei herauskommt. Sowohl der Term 8:4 ist also ein Quotient als auch das Ergebnis 4. Möchte man zwischen der Aufgabe und ihrem Ergebnis unterscheiden, spricht man vom Quotiententerm (Aufgabe) und dem Quotientenwert (Ergebnis). Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… z. B. (3:2)² = 9:4, mehr unter => Quotient potenzieren
… Mehrzahl von => Quotient
Orient
Morgenland
Sol oriens ist Latein für die aufgehende Sonne. Im antiken römischen Weltbild sah man Rom als die Mitte der Welt an. Was von Rom aus in Richtung der aufgehenden Sonne lag, nannt man entsprechend den Orient. Das waren die Länder östlich von Rom. Das deutsche Wort für den Orient ist => Morgenland
Anteil zu einem Zeitpunkt
Im Sommer 2020 lag der Anteil von Mädchen an Abiturienten im Bundesland Nordrhein-Westfalen bei 55 %. Das war dann die Mädchenquote der Abiturienten: Als Quote bezeichnet man einen Anteil zu einem bestimmten Zeitpunkt. Bezieht man einen Anteil auf ene Zeitdauer, spricht man von einer => Rate
Sekantenverfahren
Das Verfahren liefert die erste Ableitung an einem Punkt für eine Funktion, also f'(x). Gebräuchliche Namen sind auch Ableiten über den Differentialquotienten oder die h-Methode. Das Verfahren ist ausführlich beschrieben unter => Sekantenverfahren
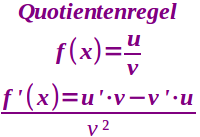Ableiten über Quotientenregel
Ist nötig, wenn x in Zähler und Nenner steht
Hat man einen Funktionsterm, bei dem das x sowohl im Zähler als auch im Nenner auftaucht, dann kann man die Quotientenregel benutzen. => Ganzen Artikel lesen …
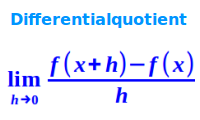Differentialquotient
dy/dx
Der Begriff spielt eine Rolle bei der Bestimmung der Tangententsteigung beziehungsweise der ersten Ableitung einer Funktion. Er wird hergeleitet aus einem Steigungsdreieck. => Ganzen Artikel lesen …
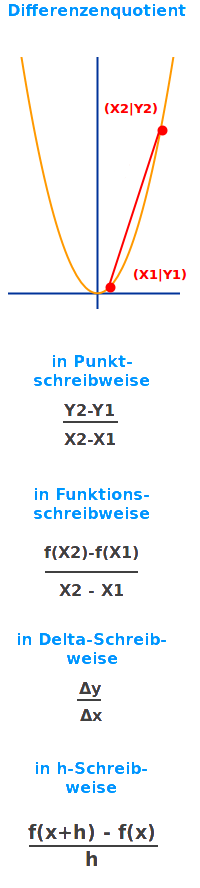
Differenzenquotient
Y2-Y1 durch X2-X1
Der Differenzenquotient dient der Berechnung der durchschnittlichen Steigung m zwischen zwei Punkten eines Graphen. Der Name kommt daher, dass man eine Differenz (Y2-Y1) durch eine andere Differenz (X2-X1) dividiert (Quotient). Eine kurze Schreibweise ist auch ΔY/ΔX, wobei das griechische Delta für Differenz steht. Er dient auch zum Berechnen der ersten Ableitung f'(x) über das Sekantenverfahren (h-Methode). => Ganzen Artikel lesen …
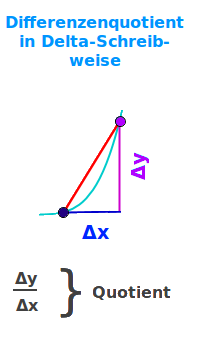
Differenzenquotient in Delta-Schreibweise
…ΔX
Zur Berechnung der Geraden einer Steigung oder von anderen Funktionen verwendet man unter anderem den Differenzenquotient (Y2-Y1)/(X2-X1). Diesen Quotienten schreibt man kurz auch mit dem griechischen Buchstaben Delta als: ΔY/ΔX. Das ist hier erklärt. => Ganzen Artikel lesen …
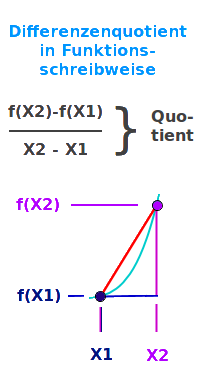Differenzenquotient in Funktionsschreibweise
Steigung
(f(x2)-f(x1)) durch (x2-x1) - das ist der Differenzenquotient in Funktionsschreibweise. Dieselbe Bedeutung haben (Y2-Y1)/(X2-X1) oder ΔY-ΔX. Das ist hier erklärt. => Ganzen Artikel lesen …
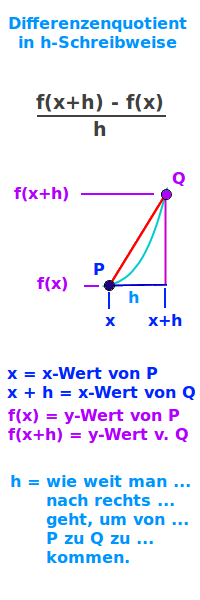Differenzenquotient in h-Schreibweise
(f(x+h)-f(x))/h
Zur Berechnung der Steigung einer Funktion in einem Punkt kann man die sogenannte h-Methode verwenden. Dabei erstellt man am Anfang den Differenzquotienten in h-Schreibweise. Das ist hier erklärt. => Ganzen Artikel lesen …
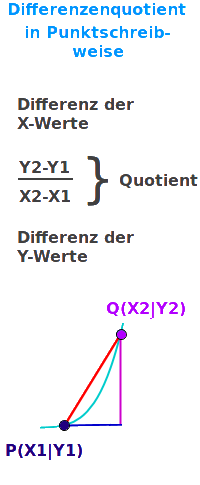Differenzenquotient in Punktschreibweise
(Y2-Y1)/(X2-X1)
Die Steigung einer Geraden oder einer Funktion in einem Punkt: in beiden Fällen kann man zur Berechnung den Differenzenquotienten verweden. Von mehreren Schreibweisen ist die Punktschreibweise eine Variante. Diese ist hier erklärt. => Ganzen Artikel lesen …
Altrnativen zu (Y2-Y1):(X2-X1)
(Y2-Y1):(X2-X1) - neben dieser Schreibweise gibt es noch viele weitere etwa mit Delta (δ, Δ), in Funktionsscheibweise oder speziell für die h-Methode (ableiten). Diese Versionen sind hier kurz aufgelistet. => Ganzen Artikel lesen …
… wie x³ zu 6, mehr unter => dritte Ableitung bilden
… wie x² zu Siehe unter => erste Ableitung bilden
… als Probe für Proportionalität, siehe unter => Quotientengleichheit
… als Probe für Proportionalität, siehe unter => Quotientengleichheit
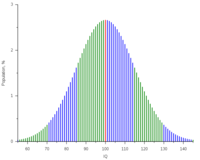Intelligenzquotient
Messung
Der Intelligenzquotient, kurz IQ, wird mit Hilfe standardisierter Tests durch Psychologen bestimmt. Tests können über mehrere Stunden hinweg dauern und eine Vielzahl von Fähigkeiten überprüfen. Als Endresultat werden aber alle Teilegebnisse zu einer einzelnen Zahl, dem IQ-Wert verdichtet. => Ganzen Artikel lesen …
=> Ganzen Artikel lesen …
.png "Eine Leiter (schwarz) wird schräg an eine senkrechte Hauswand gestellt. Dadurch entsteht ein rechtwinkliges Dreieck. Die Längen der drei Seiten können dann über den Satz des Pythagoras in Beziehung zueinander gesetzt werden.")
Leiterstellversuch (Differenzenquotient)
Analysis
Eine Leiter wird an eine senkrechte Hauswand angelehnt. Wenn man dann den Fußpunkt der Leiter auf dem Boden etwas hin und her schiebt (∆x), dann verändert sich auch die Höhe des oberen Endes der Leiter an der Hauswand (∆y). Wie groß diese Änderung von y im Verhältnis zur Änderung von x ist, das ist die anschauliche Bedeutung des Differenzenquotienten. Es wird auch erklärt, wie aus dem Differenzenquotienten der Differentialquotient und die erste Ableitung f'(x) entstehen. => Ganzen Artikel lesen …
… z. B. (3:2)² = 9:4, mehr unter => Quotient potenzieren
… z. B. (3:2)² = 9:4, mehr unter => Quotient potenzieren
… wie etwa 2^5 durch Siehe unter => Potenz durch Potenz
… wie etwa 2^5 durch Siehe unter => Potenz durch Potenz
… siehe unter => Wurzel durch Wurzel
… siehe unter => Wurzel durch Wurzel
… wie etwa 2^5 durch Siehe unter => Potenz durch Potenz
… siehe unter => Wurzel durch Wurzel
… in der Analysis, siehe unter => Differenzenquotient
… z. B. (3:2)² = 9:4, mehr unter => Quotient potenzieren
… z. B. (3:2)² = 9:4, mehr unter => Quotient potenzieren
… z. B. (3:2)² = 9:4, mehr unter => Quotient potenzieren
… wie etwa 2^5 durch Siehe unter => Potenz durch Potenz
… wie etwa 2^5 durch Siehe unter => Potenz durch Potenz
